数组
寻找数组中第k大的元素
思路1:堆。创建一个大根堆,将所有数组中的元素加入堆中,并保持堆的大小小于等于k。这样,堆中就保留了前k个最大的元素。1
2
3
4
5
6def findKthLargest(self, nums: List[int], k: int) -> int:
import heapq
if k>len(nums):
return 0
res = heapq.nlargest(k, nums)
return res[-1]
思路2:快排。使用划分算法将基准值放在数组中的合适位置 pos。将小于基准值的元素移到左边,大于等于基准值的元素移到右边。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21def findKthLargest(self, nums: List[int], k:int) -> int:
def partition(nums, left, right):
pivot = nums[left]
j = left
for i in range(left+1, right+1):
if nums[i] < pivot:
j += 1
nums[i], nums[j] = nums[j], nums[i]
nums[left], nums[j] = nums[j], nums[left]
return j
size = len(nums)
target = size - k
left, right = 0, size - 1
while True:
minIndex = partition(nums, left, right)
if minIndex == target:
return nums[minIndex]
elif minIndex < target:
left = minIndex + 1
else:
right = minIndex - 11
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43class Solution {
public:
void swap(vector<int>& nums, int left, int right){
int temp = nums[right];
nums[right] = nums[left];
nums[left] = temp;
}
int partition(vector<int>& nums, int left, int right){
int pivot = nums[left];
int j = left;
for(int i=left+1; i<=right; i++){
if (nums[i] <pivot){
j++;
swap(nums, i, j);
}
}
swap(nums, left, j);
return j;
}
int findKthLargest(vector<int>& nums, int k) {
int size = nums.size();
int target = size - k;
int left = 0;
int right = size-1;
while(true){
int midIndex = partition(nums, left, right);
if(midIndex == target){
return nums[midIndex];
}
else{
if(midIndex < target){
left = midIndex + 1;
}
else{
right = midIndex - 1;
}
}
}
return 0;
}
};
寻找两个有序数组的中位数
思路1:合并两个有序数组,遍历第len/2+1个元素即中位数。由于两队列之和是偶数时,中位数为数组中间左右两个数之和的平均,故需要一个变量保存前一次遍历时的值。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18def findMedianSortedArrays(nums1, nums2):
l1 = len(nums1)
l2 = len(nums2)
l = l1 + l2
pre, cur = -1, -1
p1, p2 = 0, 0
for i in range(l // 2 + 1):
pre = cur
if p1 < l1 and (p2 >= l2 or nums1[p1] < nums2[p2]):
cur = nums1[p1]
p1 += 1
else:
cur = nums2[p2]
p2 += 1
if l % 2 == 0:
return (pre + cur) / 2.0
else:
return cur
时间复杂度是O(l1+l2),如果要求时间复杂度为O(log(l1+l2)),则优化算法如下。
假设我们有两个数组:num1: [a1,a2,a3,…an],nums2: [b1,b2,b3,…bn]。则合并后的数组为:[nums1[:left1],nums2[:left2] | nums1[left1:], nums2[left2:]]。只要保证左右两边 个数 相同,中位数就在 | 这个边界旁边产生。
如何找边界值,我们可以用二分法,我们先确定 num1 取 m1 个数的左半边,那么 num2 取 m2 = (m+n+1)/2 - m1 的左半边,找到合适的 m1,就用二分法找。
youyu左半部分最大的值小于等于右半部分最小的值 max ( nums1[left1 - 1], nums2[left2 - 1]))<= min(nums1[left1], nums2[left2]))
因为nums1数组和nums2数组是有序的,所以nums1[left1-1]<=nums1[left],nums2[left2-1]<=left[left2],故只需保证nums2[left2-1]<=nums1[left1]和nums1[left1-1]<=nums2[left2]。
若nums2[left2-1]>nums1[left],并且为了不越界,我们需要增加left1。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30def findMedianSortedArraysII(nums1, nums2):
if len(nums1)>len(nums2):
nums1, nums2 = nums2, nums1
l1, l2 = len(nums1), len(nums2)
mid = (l1+l2+1)//2
left, right = 0, l1
while left<right:
mid1 = left+(right-left)//2
mid2 = mid - mid1
if nums1[mid1]<nums2[mid2-1]:
left = mid1+1
else:
right = mid1
mid1 = left
mid2 = mid - mid1
if mid1 == 0:
max_out_left = nums2[mid2-1]
elif mid2 == 0:
max_out_left = nums1[mid1-1]
else:
max_out_left = max(nums1[mid1-1], nums2[mid2-1])
if (l1+l2)%2 == 1:
return max_out_left
if mid1 == l1:
min_out_right = nums2[mid2]
elif mid2 == l2:
min_out_right = nums1[mid1]
else:
min_out_right = min(nums1[mid1], nums2[mid2])
return (max_out_left+min_out_right)/2.0
连续子数组的最大和
思路:数组有正有负的情况,这时我们遍历数组,累计求和total, 如果total小于0,则直接舍弃前面的和,重新从0开始计算,确保子数组和最大。1
2
3
4
5
6
7
8
9
10
11
12def maxSubArray(self, nums: List[int]) -> int:
if not nums:
return 0
nsum = 0
ans = float("-inf")
for num in nums:
if nsum>=0:
nsum += num
else:
nsum = num
ans = max(ans, nsum)
return ans
最长连续递增序列
给定一个未经排序的整数数组,找到最长且连续的递增序列。
输入:[1,3,5,4,7],最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为5和7在原数组里被4隔开。
思路:从 0 位置开始遍历,遍历时根据前后元素状态判断是否递增,递增则 count++,递减则 count=1。如果 count>ans,则更新 ans,直到循环结束。1
2
3
4
5
6
7
8
9
10
11def findLengthOfLCIS(self, nums: List[int]) -> int:
if len(nums)<=1:
return len(nums)
ans, count = 1, 1
for i in range(len(nums)-1):
if nums[i+1]>nums[i]:
count += 1
else:
count = 1
ans = max(ans, count)
return ans
最长上升子序列
给定一个无序的整数数组,找到其中最长上升子序列的长度。
输入:[10,9,2,5,3,7,101,18],最长的上升子序列是 [2,3,7,101],它的长度是 4。
思路一:动态规划
dp[i] 的值代表 nums 前i个数字的最长子序列长度。当 nums[i] > nums[j] 时: nums[i] 可以接在 nums[j] 之后(此题要求严格递增),此情况下最长上升子序列长度为 dp[j] + 1 ;实现方式为遍历 j 时,每轮执行 dp[i] = max(dp[i], dp[j] + 1)。1
2
3
4
5
6
7
8
9def lengthOfLIS(self, nums: List[int]) -> int:
if not nums:
return 0
dp = [1]*len(nums)
for i in range(len(nums)):
for j in range(i):
if nums[j]<nums[i]:
dp[i] = max(dp[i], dp[j]+1)
return max(dp)
思路二:动态规划+二分查找
动态规划中,通过线性遍历来计算 dpdp 的复杂度无法降低;
每轮计算中,需要通过线性遍历 [0,k) 区间元素来得到 dp[k] 。我们考虑:是否可以通过重新设计状态定义,使整个 dp 为一个排序列表;这样在计算每个 dp[k] 时,就可以通过二分法遍历 [0,k) 区间元素,将此部分复杂度由 O(N) 降至 O(logN)。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18def lengthOfLIS(self, nums: List[int]) -> int:
n = len(nums)
if n<2:
return n
res = [nums[0]]
for num in nums[1:]:
if num>res[-1]:
res.append(num)
continue
left, right = 0, len(res)-1
while left<right:
mid = left+(right-left)//2
if res[mid]<num:
left = mid+1
else:
right = mid
res[left] = num
return len(res)
最长连续序列
给定一个未排序的整数数组,找出最长连续序列的长度。
输入: [100, 4, 200, 1, 3, 2],最长连续序列是 [1, 2, 3, 4],它的长度为 4。
思路:对每个元素进行判断,是不是序列的开始。即nums[i]-1是否在哈希表中(O(1)的时间)。
如果nums[i]-1在set中,说明不是序列的开始,则跳过。
如果nums[i]-1不在,说明nums[i]是序列的开始。判断nums[i]+1是否在哈希集合中,直到没有出现在集合中,判断此时的长度cur_len。和最长序列长度进行比较,max_len = max(curr_len,max_len)。1
2
3
4
5
6
7
8
9
10
11
12
13
14def longestConsecutive(self, nums: List[int]) -> int:
if not nums:
return 0
s = set(nums)
maxlen = 0
for num in s:
curlen = 1
if num-1 in s:
continue
while num+1 in s:
num += 1
curlen += 1
maxlen = max(maxlen, curlen)
return maxlen
滑动窗口
什么是滑动窗口?其实就是一个队列,比如题目无重复字符的最长子串中的abcabcbb,进入这个队列(窗口)为abc满足题目,当再进入a,队列就变成了abca,这时候不满足要求。所以,我们就要移动这个队列。我们只要把队列的左边元素移出就行,直到满足题目要求。
例题1:leetcode3.无重复字符的最长子串(滑窗模板)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21def lengthOfLongestSubstring(s):
from collections import defaultdict
if not s:
return 0
if len(s)==1:
return 1
left, right, counter= 0, 0, 0
maxLen = 0
windows = defaultdict(int)
while right<len(s):
if windows[s[right]]>0:
counter += 1
windows[s[right]] += 1
right += 1
while counter>0: # 窗口条件决定左边元素是否移出
if windows[s[left]]>1:
counter -= 1
windows[s[left]] -= 1
left += 1
maxLen = max(maxLen, right-left)
return maxLen
例题:
76.最小覆盖子串
209.长度最小的子数组
567.字符串的排列
二叉树
前序
递归1
2
3
4
5
6def preOrder(node):
if not node:
return None
print(node.val)
preOrder(node.left)
preOrder(node.right)
非递归1
2
3
4
5
6
7
8
9def preOrder(node):
stack = [node]
while stack:
print(node.val)
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
node = stack.pop()
中序遍历
递归1
2
3
4
5
6def inorder(node):
if not node:
return None
inorder(node.left)
print(node.val)
inorder(node.right)
非递归1
2
3
4
5
6
7
8
9def inorder(node):
stack = []
while node or len(stack)>0:
while node:
stack.append(node)
node = node.left
node = stack.pop()
print(node.val)
node = node.right
后序遍历
递归1
2
3
4
5
6def postOrder(node):
if not node:
return None
postOrder(node.left)
postOrder(node.right)
print(node.val)
非递归:使用两个栈结构,第一个栈进栈顺序:左节点->右节点->根节点,第一个栈弹出顺序:根节点->右节点->左节点,第二个栈存储为第一个栈的每个弹出依次入栈,最后第二个栈依次出栈。1
2
3
4
5
6
7
8
9
10
11
12def postOrder(node):
stack = [node]
stack2 = []
while len(stack)>0:
node = stack.pop()
stack2.append(node)
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
while len(stack2)>0:
print(stack2.pop().val)
层次遍历
1 | if not node: |
验证二叉搜索树
买卖股票
1)给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票),求获得的最大利润。
思路1:只要用一个变量记录一个历史最低价格 minprice,我们就可以假设自己的股票是在那天买的。那么我们在第 i 天卖出股票能得到的利润就是 prices[i] - minprice。1
2
3
4
5
6
7def maxProfit(self, prices: List[int]) -> int:
minprice = float("inf")
maxprofit = 0
for price in prices:
maxprofit = max(price - minprice, maxprofit)
minprice = min(price, minprice)
return maxprofit
思路2:dp[i][j]表示第i天用户持股为j所获最大利润。
j只有两个值:0表示不持股,1表示持股。
则dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1], -prices[i]),因为题目只允许一次交易,因此不能加上dp[i-1][0]
初始值:第0天不持股,dp[0][0]=0;第0天持股,dp[0][1]=-prices[0]1
2
3
4
5
6
7
8
9
10
11def maxProfit(prices):
if len(prices)<2:
return 0
n = len(prices)
dp = [[0]*n for _ in range(2)]
dp[0][0] = 0
dp[0][1] = -prices[0]
for i in range(1, n):
dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1], -prices[i])
return dp[-1][0]
考虑状态压缩,dp[i]仅仅依赖于dp[i-1]1
2
3
4
5
6
7
8
9
10
11def maxProfit2(prices):
n = len(prices)
if n<2:
return 0
dp = [0]*2
dp[0] = 0
dp[1] = -prices[0]
for i in range(1, n):
dp[0] = max(dp[0], dp[1]+prices[i])
dp[1] = max(dp[1], -prices[i])
return dp[0]
2)可以尽可能地完成更多的交易(多次买卖一支股票),但不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)
思路:dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i])
dp[0][0] = 0, dp[0][1] = -prices[0]1
2
3
4
5
6
7
8
9
10
11def maxProfitII(prices):
n = len(prices)
if n<2:
return 0
dp = [[0]*2 for _ in range(n)]
dp[0][0] = 0
dp[0][1] = -prices[0]
for i in range(1, n):
dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i])
return dp[-1][0]
考虑状态压缩 dp[i]也仅仅依赖dp[i-1]
3)最多可以完成两笔交易。
注:必须在再次购买前出售掉之前的股票
思路:重新定义状态方程
dp[i][0]表示未交易
dp[i][1]表示第一次买入一支股票
dp[i][2]表示第一次卖出一支股票
dp[i][3]表示第二次买入一支股票
dp[i][4]表示第二次卖出一支股票
状态转移方程见代码
初始化:第0天初始化为前两个状态,而状态3(第二次持股)只能赋值为一个不可能的数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15def maxProfitIII(prices):
n = len(prices)
if n<2:
return 0
dp = [[0]*5 for _ in range(n)]
dp[0][1] = -prices[0]
for i in range(n):
dp[i][3] = float("-inf")
for i in range(1, n):
dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i])
dp[i][2] = max(dp[i-1][2], dp[i-1][1]+prices[i])
dp[i][3] = max(dp[i-1][3], dp[i-1][2]-prices[i])
dp[i][4] = max(dp[i-1][4], dp[i-1][3]+prices[i])
# 最大值只发生在不持股的时候
return max(0, dp[-1][2], dp[-1][4])
状态压缩,dp[i]仅仅依赖于dp[i-1]
4)最多可以完成 k 笔交易
注:必须在再次购买前出售掉之前的股票
5)在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
a) 必须在再次购买前出售掉之前的股票;
b) 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)
思路:增加一个状态,j取三个值:
0表示不持股,1表示持股,2表示冷冻期
状态转移方程:
dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][2]-prices[i])
dp[i][2] = dp[i-1][0]1
2
3
4
5
6
7
8
9
10
11def maxProfitV(prices):
n = len(prices)
if n<2:
return 0
dp = [[0]*3 for _ in range(n)]
dp[0][1] = -prices[0]
for i in range(1, n):
dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][2]-prices[i])
dp[i][2] = dp[i-1][0]
return max(dp[-1][0], dp[-1][2])
考虑状态压缩,dp[i]仅仅只依赖于dp[i-1]
6)你可以无限次地完成交易,但是你每次交易都需要付手续费fee。
如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
思路:规定手续费在买入股票时扣除
状态转移方程:
dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i]-fee)1
2
3
4
5
6
7
8
9
10def maxProfitVI(prices, fee):
n = len(prices)
if n<2:
return 0
dp = [[0]*2 for _ in range(n)]
dp[0][1] = -prices[0]-fee
for i in range(1, n):
dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i]-fee)
return dp[-1][0]
动态规划
最长回文子串
给定一个字符串s,找到s中最长的回文子串。
例:输入:”babad”,输出为:”bab”。
思路:设dp[i][j]表示子串s[i,j]是否为回文子串,则状态转移方程为:dp[i][j] = (s[i]==s[j]) and dp[i+1][j-1]。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18def longestPalindrome(self, s: str) -> str:
if not s or len(s)==1:
return s
n = len(s)
dp = [[0]*n for _ in range(n)]
left, right = 0, 0
maxLen = 0
for j in range(n):
dp[j][j] = 1
for i in range(j):
if s[i]==s[j] and (j-i<2 or dp[i+1][j-1]==1):
dp[i][j] = 1
else:
dp[i][j] = 0
if dp[i][j]==1 and maxLen<j-i+1:
maxLen = j-i+1
left, right = i, j
return s[left:right+1]
最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列。
实例:输入text1 = “abcde”, text2 = “ace” ,输出3。最长公共子序列是 “ace”,它的长度为 3。
思路:设dp[i][j]是text1[:i]和text2[:j]的最长公共子序列长度,则状态转移方程为:dp[i][j] = dp[i-1][j-1]+1 if text1[i]==text2[j] else max(dp[i-1][j], dp[i][j-1])。1
2
3
4
5
6
7
8
9
10def longestCommonSubsequence(self, text1: str, text2: str) -> int:
m, n = len(text1), len(text2)
dp = [[0]*(n+1) for _ in range(m+1)]
for i in range(1, m+1):
for j in range(1, n+1):
if text1[i-1] == text2[j-1]:
dp[i][j] = dp[i-1][j-1]+1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[-1][-1]
最长公共子串
给出两个字符串str1,str2返回该两个字符串的最长公共子串。
实例:输入str1 = “1AB2345CD”,str2 = “12345EF”,输出“2345”。
思路:dp[i][j]的含义为以str1[i]和str2[j]结尾的最长公共子串,则状态转移方程为dp[i][j]=dp[i-1][j-1]+1 if str1[i]==str2[j] else 0.1
2
3
4
5
6
7
8
9
10def longestCommonSubstring(self, str1: str, str2: str) -> int:
m, n = len(str1), len(str2)
dp = [[0]*(n+1) for _ in range(m+1)]
for i in range(1, m+1):
for j in range(1, n+1):
if str1[i-1] == str2[j-1]:
dp[i][j] = dp[i-1][j-1]+1
else:
dp[i][j] = 0
return dp[-1][-1]
编辑距离
给你两个单词word1和word2,请你计算出将word1转换为word2所使用的最少操作数。
你可以对一个单词进行如下三种操作:
1)插入一个字符;2)删除一个字符;3)替换一个字符。
示例:输入word1 = “horse”, word2 = “ros”,输出为3。
思路:dp[i][j] 代表 word1 到 i 位置转换成 word2 到 j 位置需要最少步数。所以,当 word1[i] == word2[j],dp[i][j] = dp[i-1][j-1];当 word1[i] != word2[j],dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1。其中,dp[i-1][j-1] 表示替换操作,dp[i-1][j] 表示删除操作,dp[i][j-1] 表示插入操作。1
2
3
4
5
6
7
8
9
10
11
12
13
14def minDistance(self, word1: str, word2: str) -> int:
n1, n2 = len(word1), len(word2)
dp = [[0]*(n2+1) for _ in range(n1+1)]
for j in range(1, n2+1):
dp[0][j] = dp[0][j-1]+1
for i in range(1, n1+1):
dp[i][0] = dp[i-1][0]+1
for i in range(1, n1+1):
for j in range(1, n2+1):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])+1
return dp[-1][-1]
让字符串成为回文串的最少插入次数
给你一个字符串 s ,每一次操作你都可以在字符串的任意位置插入任意字符。请你返回让 s 成为回文串的 最少操作次数 。
示例:输入s = “mbadm”,输出为2。字符串可变为 “mbdadbm” 或者 “mdbabdm” 。
思路:是最长公共子序列的变形。当前字符串要变成回文,那只要把不一样的找出来就好了。即:求出反过来的字符串和当前字符串的最长公共子序列,然后用字符串长度减去最长公共子序列长度即可。1
2
3
4
5
6
7
8
9
10
11
12
13def minInsertions(self, s: str) -> int:
n = len(s)
t = s[::-1]
if s==t:
return 0
dp = [[0]*(n+1) for _ in range(n+1)]
for i in range(1, n+1):
for j in range(1, n+1):
if s[i-1] == t[j-1]:
dp[i][j] = dp[i-1][j-1]+1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return n-dp[-1][-1]
零钱兑换
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。
示例:输入coins = [1, 2, 5], amount = 11,输出3。11可拆分成5+5+1。
思路: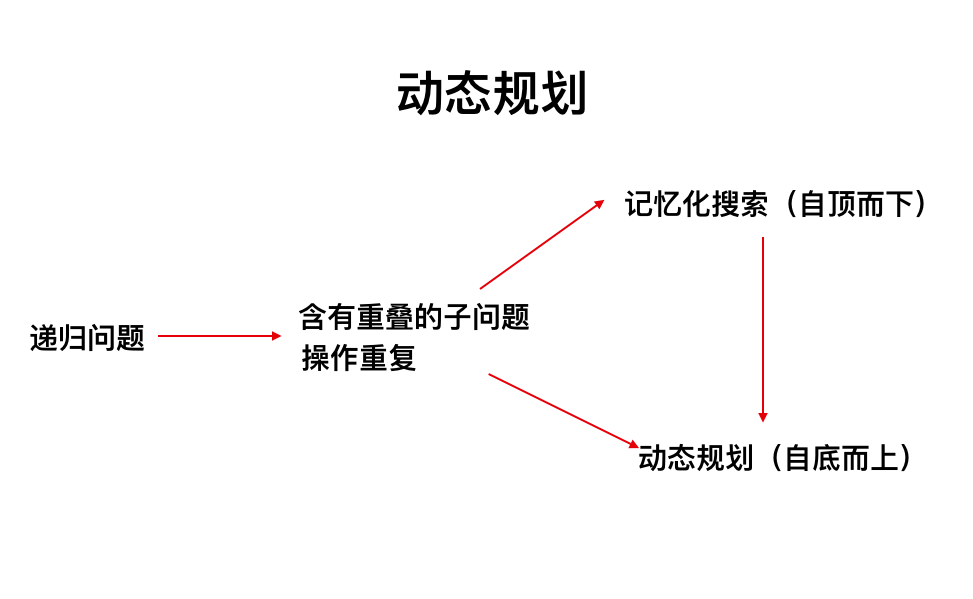
回溯:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 def coinChange(self, coins: List[int], amount: int) -> int:
if not coins:
return -1
res = [float("inf")]
def dfs(coins, amount, count, res):
if amount == 0:
res[0] = min(res[0], count)
for coin in coins:
diff = amount-coin
if diff<0:
break
dfs(coins, diff, count+1, res)
dfs(coins, amount, 0, res)
return res[0] if res[0]!=float("inf") else -1
```
在回溯法中,如果含有很多的重复的计算的时候,就可以使用记忆化的搜索,将可能出现的重复计算大状态使用一个数组来保存其值,在进行重复的计算的时候,就可以直接的调用数组中的值,较少了不必要的递归。使用了记忆化搜索后,一般还可以进行优化,在记忆化搜索的基础上,变成 自底而上 的动态规划。
若包含当前的 coins[i],那么剩余钱就是 i-coins[i],这种操作要兑换的硬币数是 memo[i-coins[j]] + 1。
```Python
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [float("inf")]*(amount+1)
dp[0] = 0
for i in range(1,amount+1):
for coin in coins:
if i >= coin:
dp[i] = min(dp[i], dp[i-coin]+1)
return dp[-1] if (dp[-1]!=float("inf")) else -1
不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。问总共有多少条不同的路径?
思路:令 dp[i][j] 是到达 i, j 最多路径,则动态转移方程为:dp[i][j] = dp[i-1][j] + dp[i][j-1]。
对于第一行 dp[0][j],或者第一列 dp[i][0],由于都是在边界,所以只能为 1。1
2
3
4
5
6
7
8
9
10def uniquePaths(self, m: int, n: int) -> int:
dp = [[0]*n for _ in range(m)]
for i in range(1, m):
dp[i][0] = 1
for i in range(1, n):
dp[0][i] = 1
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i-1][j]+dp[i][j-1]
return dp[-1][-1]
空间复杂度为O(mn),由于当前位置只和该位置左边和上方的变量有关,故空间复杂度可优化为O(n)1
2
3
4
5
6def uniquePaths(self, m: int, n: int) -> int:
dp = [1] * n
for i in range(1, m):
for j in range(1, n):
dp[j] = dp[j]+dp[j-1]
return dp[-1]
礼物的最大价值
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
思路:令dp[i][j]为位置[i,j]的礼物价值,则动态转移方程为:dp[i][j] = max(dp[i-1][j], dp[i][j-1])+gift[i][j]。1
2
3
4
5
6
7
8
9
10
11
12def maxValue(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
dp = [[0]*n for _ in range(m)]
dp[0][0] = grid[0][0]
for i in range(1, m):
dp[i][0] = dp[i-1][0]+grid[i][0]
for j in range(1, n):
dp[0][j] = dp[0][j-1]+grid[0][j]
for i in range(1, m):
for j in range(1, n):
dp[i][j] = max(dp[i-1][j], dp[i][j-1])+grid[i][j]
return dp[-1][-1]
打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
思路:和拿糖果问题类似。设dp[i]为抢劫第i间房间的最大金额,np[i]为不抢劫第i间房间的最大金额。则动态转移方程为:dp[i]=np[i]+nums[i],np[i] = max(np[i-1], dp[i-1])1
2
3
4
5
6
7
8
9
10
11
12
13def rob(self, nums: List[int]) -> int:
if not nums:
return 0
if len(nums)==1:
return nums[0]
n = len(nums)
dp = [0]*n
np = [0]*n
dp[0] = nums[0]
for i in range(1, n):
dp[i] = np[i-1]+nums[i]
np[i] = max(np[i-1], dp[i-1])
return max(dp)
优化,在当前位置 n 房屋可盗窃的最大值,要么就是 n-1 房屋可盗窃的最大值,要么就是 n-2 房屋可盗窃的最大值加上当前房屋的值。1
2
3
4
5
6
7
8
9
10
11def rob(self, nums: List[int]) -> int:
if not nums:
return 0
if len(nums)==1:
return nums[0]
n = len(nums)
dp = [0]*(n+1)
dp[1] = nums[0]
for i in range(2, n+1):
dp[i] = max(dp[i-1], dp[i-2]+nums[i-1])
return dp[-1]
打家劫舍II
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
思路:此题中的房间是环状排列的(即首尾相接),环状排列意味着第一个房子和最后一个房子中只能选择一个偷窃,因此可以把此环状排列房间问题约化为两个单排排列房间子问题:
1)在不偷窃第一个房子的情况下(即 nums[1:]),最大金额是p1;
2)在不偷窃最后一个房子的情况下(即 nums[:n-1]),最大金额是 p2。
设dp[i] 代表前 i 个房子在满足条件下的能偷窃到的最高金额,则dp[i] = max(dp[i-1], dp[i-2]+nums[i-1])。我们发现 dp[n] 只与 dp[n-1] 和 dp[n-2] 有关系,因此我们可以设两个变量 cur和 pre 交替记录,将空间复杂度降到 O(1)。1
2
3
4
5
6
7
8
9def rob(self, nums: List[int]) -> int:
def robCore(nums):
cur, pre = 0, 0
for num in nums:
cur, pre = max(cur, pre+num), cur
return cur
if len(nums)==1:
return nums[0]
return max(robCore(nums[:-1]), robCore(nums[1:]))
打家劫舍III
在上次打劫完一条街道之后和一圈房屋后,小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为“根”。 除了“根”之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫,房屋将自动报警。
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
思路:假设func(root)为问题的解,即能从以root为根节点的树中盗窃到的最大金额。那么以root房子开始分析,可以选择偷窃root房子,也可以选择不偷窃。如果偷窃root房子,那么func(root) = root->val + func(root->left)->unrob + func(root->left)->unrob。
如果不偷窃root房子,那么func(root) = func(root->left)->robed + func(root->right)->robed。1
2
3
4
5
6
7
8
9
10
11
12
13
14def rob(self, root: TreeNode) -> int:
def robCore(root):
if not root:
return [0, 0]
left = robCore(root.left)
right = robCore(root.right)
robed = root.val+left[1]+right[1]
unrob = left[0]+right[0]
return [max(robed, unrob), unrob]
if not root:
return 0
# res[0]偷窃该节点的金额,res[1]不偷窃该节点的金额
res = robCore(root)
return res[0]
递归
全排列
给定一个没有重复数字的序列,返回其所有可能的全排列。
思路:回溯法。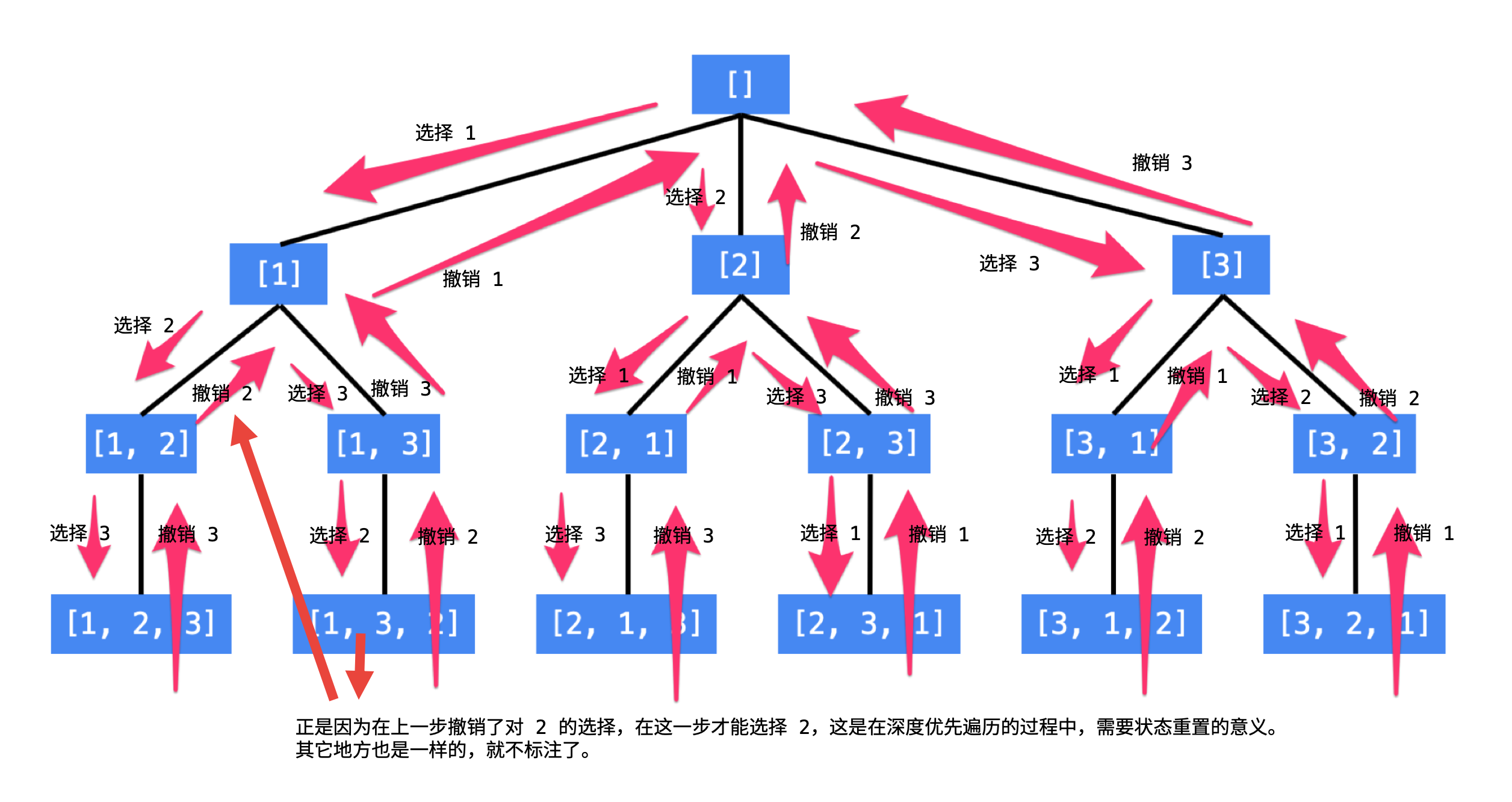
1
2
3
4
5
6
7
8
9
10
11
12
13
14def permute(self, nums: List[int]) -> List[List[int]]:
if len(nums)<=1:
return [nums]
res, stack = [], []
def backtrack(nums, stack):
if not nums:
res.append(stack[:])
return
for i in range(len(nums)):
stack.append(nums[i])
backtrack(nums[:i]+nums[i+1:], stack)
stack.pop()
backtrack(nums, stack)
return res
全排列II
给定一个可包含重复数字的序列,返回所有不重复的全排列。
示例:输入[1,1,2],输出[[1,1,2],[1,2,1],[2,1,1]]
思路:先排序,然后回溯+剪枝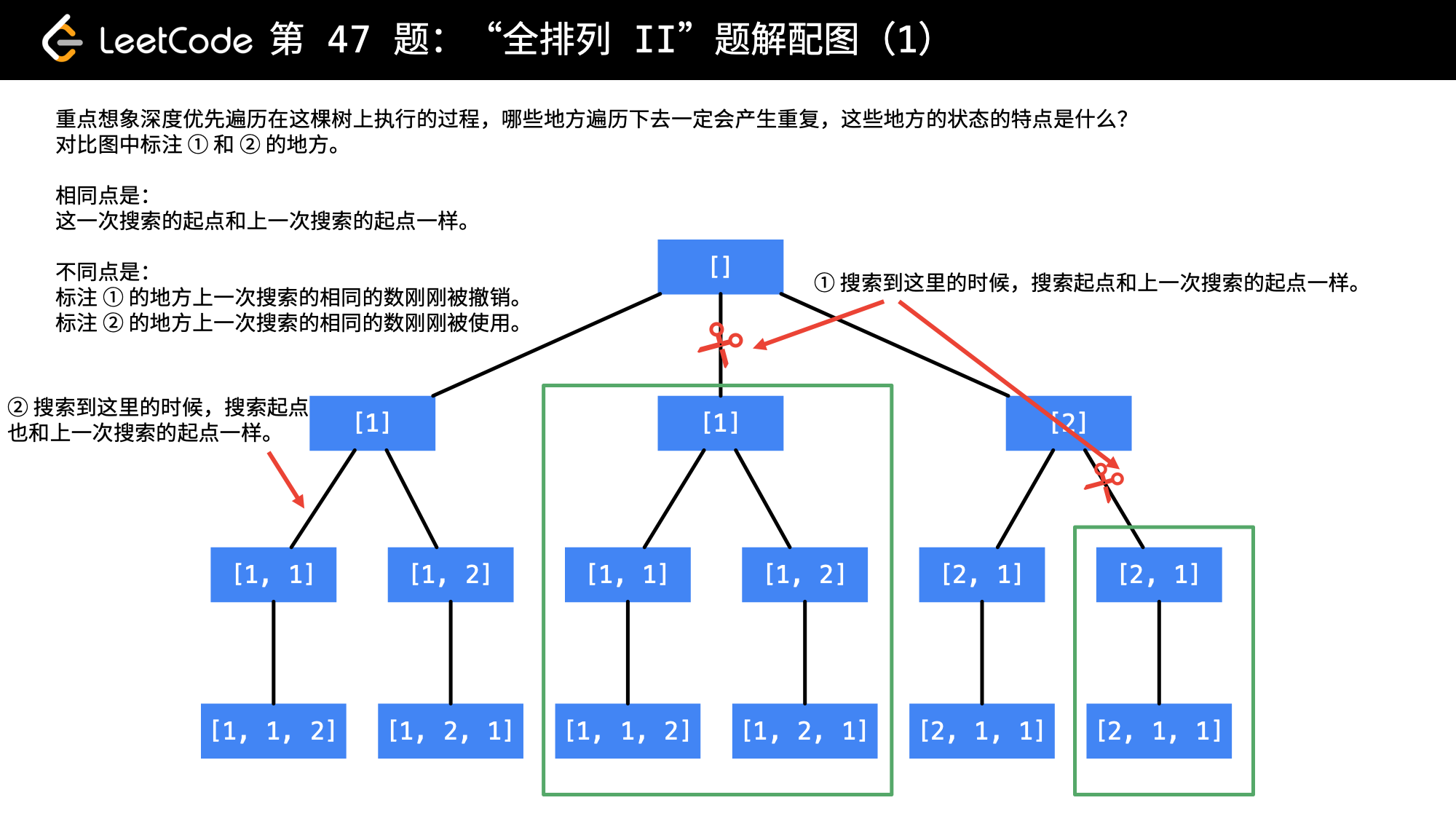
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15def permuteUnique(self, nums: List[int]) -> List[List[int]]:
res = []
nums.sort()
def backtrack(nums, tmp):
if not nums:
res.append(tmp[:])
return
for i in range(len(nums)):
if i>0 and nums[i]==nums[i-1]:
continue
tmp.append(nums[i])
backtrack(nums[:i]+nums[i+1:], tmp)
tmp.pop()
backtrack(nums, [])
return res
组合总和
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。解集不能包含重复的组合。
示例:输入candidates=[2,3,6,7],target=7,输出[[7],[2,2,3]]
思路:回溯+剪枝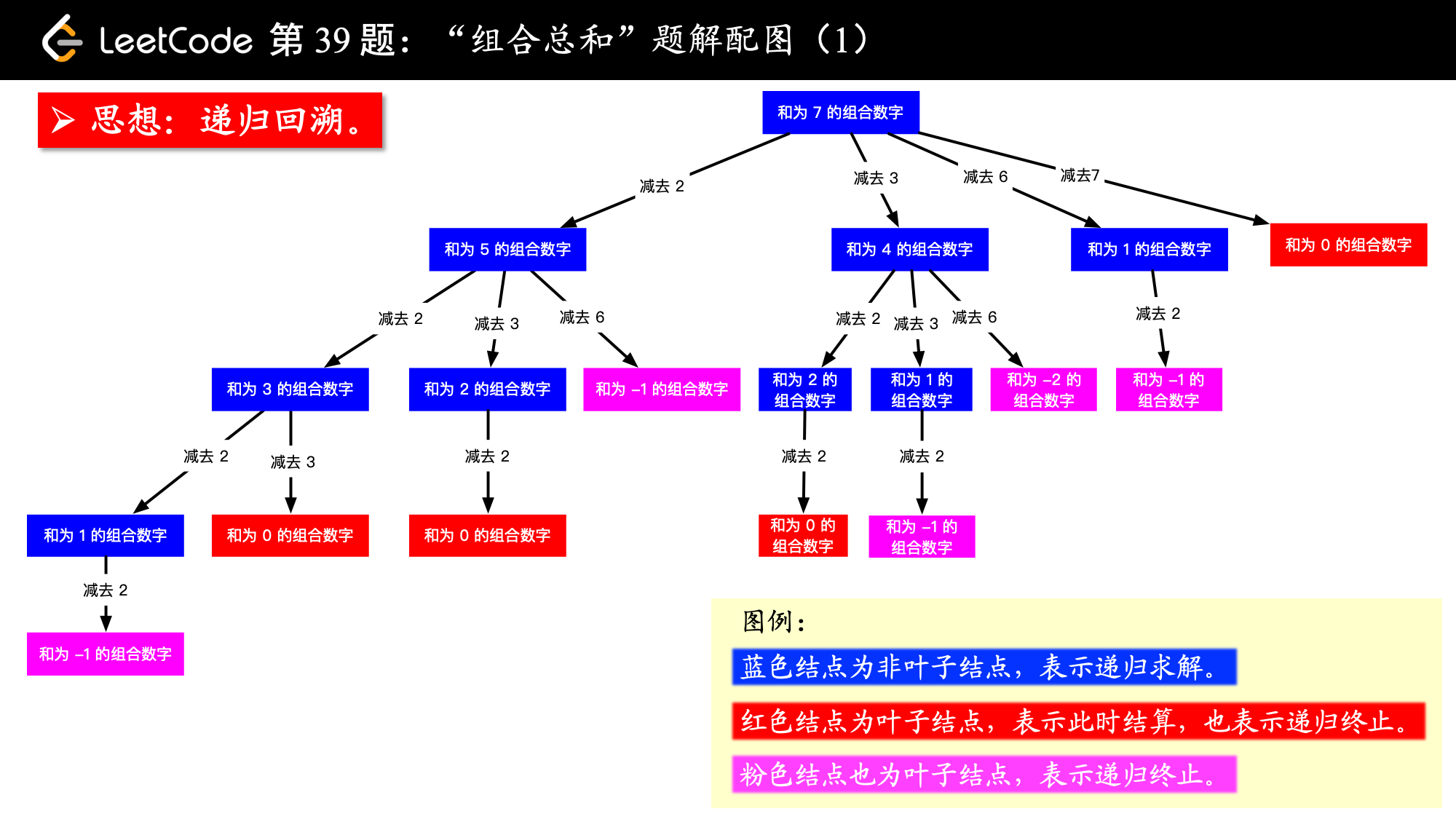
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
def dfs(nums, target, start, tmp, res):
if target==0:
res.append(tmp[:])
return
for i in range(start, len(nums)):
diff = target-nums[i]
if diff<0:
break
tmp.append(nums[i])
dfs(nums, diff, i, tmp, res)
tmp.pop()
res = []
dfs(candidates, target, 0, [], res)
return res
组合总和II
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。解集不能包含重复的组合。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
def dfs(nums, target, start, tmp, res):
if target==0:
res.append(tmp[:])
return
for i in range(start, len(nums)):
diff = target-nums[i]
if diff<0:
break
if i>start and nums[i]==nums[i-1]:
continue
tmp.append(nums[i])
dfs(nums, diff, i+1, tmp, res)
tmp.pop()
res = []
candidates.sort()
dfs(candidates, target, 0, [], res)
return res
组合总和III
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
示例:输入k=3,n=7,输出[[1,2,4]]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18def combinationSum3(self, k: int, n: int) -> List[List[int]]:
def dfs(target, k, start, path, res):
if len(path)==k and target==0:
res.append(path[:])
return
for i in range(start, 10):
diff = target-i
if diff<0:
continue
path.append(i)
dfs(diff, k, i+1, path, res)
path.pop()
if k<=0 or n<k:
return []
res = []
dfs(n, k, 1, [], res)
return res
组合总和IV
给定一个由正整数组成且不存在重复数字的数组,找出和为给定目标正整数的组合的个数。
示例:输入nums=[1,2,3],target=4,所有的可能组合为:(1, 1, 1, 1),(1, 1, 2),(1, 2, 1),(1, 3),(2, 1, 1),(2, 2),(3, 1)。
因此输出为7。
思路:背包问题,动态规划
状态转移方程:dp[i]= dp[i - nums[0]] + dp[i - nums[1]] + dp[i - nums[2]] + …,值得注意的是:dp[0] = 1,表示,如果那个硬币的面值刚刚好等于需要凑出的价值,这个就成为 1 种组合方案。1
2
3
4
5
6
7
8
9
10def combinationSum4(self, nums: List[int], target: int) -> int:
if not nums or target<=0:
return 0
dp = [0 for _ in range(target+1)]
dp[0] = 1
for i in range(1, target+1):
for num in nums:
if i >= num:
dp[i] += dp[i-num]
return dp[-1]
子集
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。解集不能包含重复的子集。
示例:输入nums = [1,2,3],输出[[3],[1],[2],[1,2,3],[1,3],[2,3],[1,2],[]]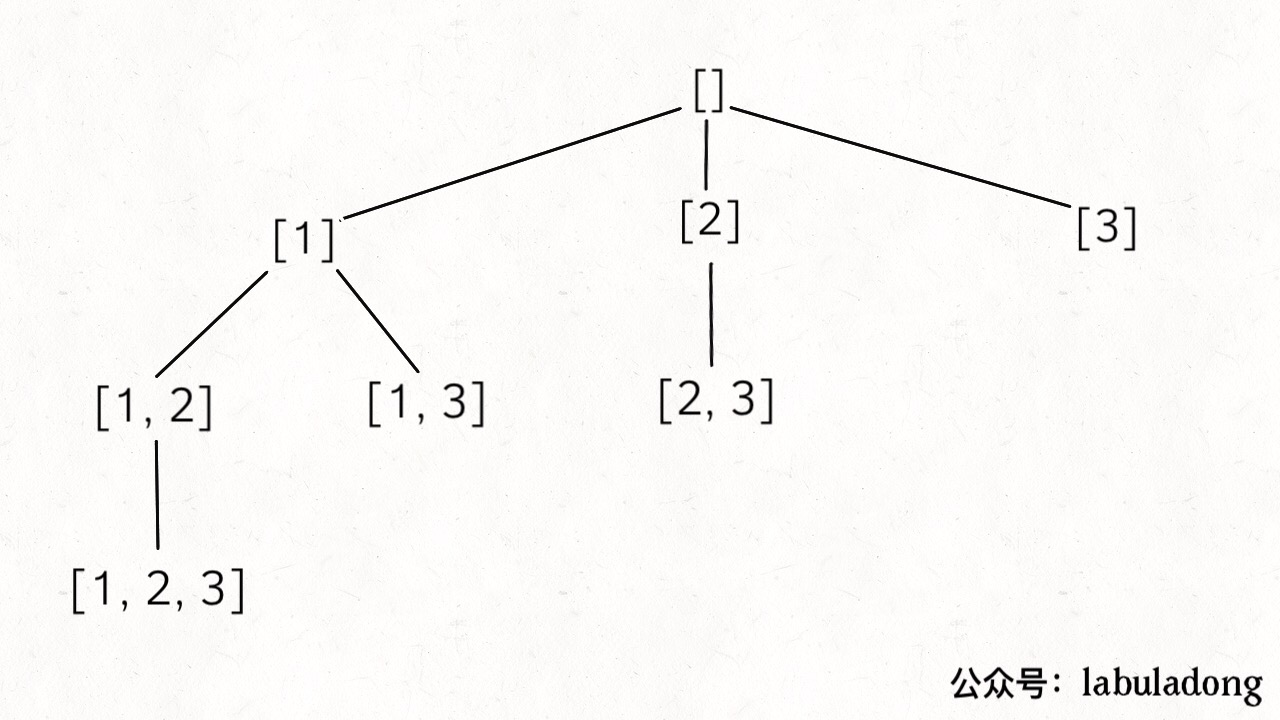
1
2
3
4
5
6
7
8
9
10def subsets(self, nums: List[int]) -> List[List[int]]:
def dfs(nums, start, tmp, res):
res.append(tmp[:])
for i in range(start, len(nums)):
tmp.append(nums[i])
dfs(nums, i+1, tmp, res)
tmp.pop()
res = []
dfs(nums, 0, [], res)
return res
子集II
定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。解集不能包含重复的子集。
示例:输入[1,2,2],输出[[2],[1],[1,2,2],[2,2],[1,2],[]]1
2
3
4
5
6
7
8
9
10
11
12
13def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
def dfs(nums, start, tmp, res):
res.append(tmp[:])
for i in range(start, len(nums)):
if i>start and nums[i]==nums[i-1]:
continue
tmp.append(nums[i])
dfs(nums, i+1, tmp, res)
tmp.pop()
res = []
nums.sort()
dfs(nums, 0, [], res)
return res
N皇后
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。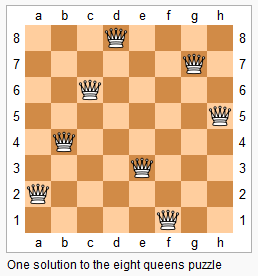
给定一个整数 n,返回 n 皇后不同的解决方案的数量。
示例:输入4,输出2,即存在两种不同的解法
思路:回溯法,存在约束条件:一行只可能有一个皇后且一列也只可能有一个皇后。对于所有的主对角线有 行号 + 列号 = 常数,对于所有的次对角线有 行号 - 列号 = 常数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22def totalNQueens(self, n: int) -> int:
def dfs(n, row, col, master, slave, path, res):
if row == n:
res[0] += 1
return
for i in range(n):
if i not in col and row+i not in slave and row-i not in master:
path.append(i)
col.add(i)
master.add(row-i)
slave.add(row+i)
dfs(n, row+1, col, master, slave, path, res)
slave.remove(row+i)
master.remove(row-i)
col.remove(i)
path.pop()
if n == 0:
return 0
res = [0]
col, master, slave = set(), set(), set()
dfs(n, 0, col, master, slave, [], res)
return res[0]
岛屿数量
给定一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,计算岛屿的数量。一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。
输入:
11110
11010
11000
00000
输出:1
思路:深度优先遍历,将遍历过的相邻岛屿修改为0,计算矩阵中不相邻的1的个数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19def numIslands(self, grid: List[List[str]]) -> int:
def dfs(grid, row, col, rows, cols):
if not 0<=row<rows or not 0<=col<cols or grid[row][col]=='0':
return
grid[row][col] = '0'
dfs(grid, row+1, col, rows, cols)
dfs(grid, row-1, col, rows, cols)
dfs(grid, row, col+1, rows, cols)
dfs(grid, row, col-1, rows, cols)
if not grid:
return 0
ans = 0
m, n = len(grid), len(grid[0])
for i in range(m):
for j in range(n):
if grid[i][j] == '1':
ans += 1
dfs(grid, i, j, m, n)
return ans
岛屿的最大面积
一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
找到给定的二维数组中最大的岛屿面积。(如果没有岛屿,则返回面积为 0 。)
思路:深度优先遍历。在一个土地上,以 4 个方向探索与之相连的每一个土地(以及与这些土地相连的土地),那么探索过的土地总数将是该连通形状的面积。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
def dfs(grid, seen, row, col, rows, cols):
if 0<=row<rows and 0<=col<cols and grid[row][col]==1 and seen[row][col]==False:
seen[row][col] = True
up = dfs(grid, seen, row-1, col, rows, cols)
down = dfs(grid, seen, row+1, col, rows, cols)
left = dfs(grid, seen, row, col-1, rows, cols)
right = dfs(grid, seen, row, col+1, rows, cols)
return up+down+left+right+1
else:
return 0
if not grid:
return 0
m, n = len(grid), len(grid[0])
seen = [[False]*n for _ in range(m)]
maxArea = 0
for i in range(m):
for j in range(n):
if grid[i][j]==1:
curArea = dfs(grid, seen, i, j, m, n)
maxArea = max(maxArea, curArea)
return maxArea
最大正方形面积
给定01矩阵
0 1 0 1 1 1
1 0 1 1 1 0
1 1 0 1 1 1
输出最大正方形面积,上面的例子面积是4。1
2
3
4
5
6
7
8
9
10
11
12
13def findMaxSquare(nums):
if not nums or not nums[0]:
return 0
rows = len(nums)
cols = len(nums[0])
l = 0
dp = [[0]*(cols+1) for _ in range(rows+1)]
for i in range(1, rows+1):
for j in range(1, cols+1):
if nums[i-1][j-1] == 1:
dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])+1
l = max(dp[i][j], l)
return l*l