深度学习基础知识

深度学习

SGD,Momentum,Adagard,Adam原理

1. SGD、BGD和Mini-BGD:

SGD(stochastic gradient descent):随机梯度下降，算法在每读入一个数据都会立刻计算loss function的梯度来更新参数，假设loss function为L(w),下同。

$$w-=\eta \bigtriangledown_{w_{i}}L(w_{i})$$

优点：收敛的速度快，可以实现在线更新
缺点：很容易陷入到局部最优，困在马鞍点
BGD(batch gradient decent):批量梯度下降，算法在读取整个数据集后累加来计算损失函数的梯度。

$$w-=\eta \bigtriangledown_{w}L(w)$$

优点：如果loss function为convex(凸函数)，则基本可以找到全局最优解
缺点：数据处理量大，导致梯度下降慢；不能实时增加实例，在线更新；训练占内存
Mini-BGD(mini-batch gradient descent):选择小批量数据进行梯度下降，这是一个折中的方法，采用训练集的子集(mini-batch)来计算loss function的梯度：

$$w-=\eta \bigtriangledown_{w_{i:i+n}}L(w_{i:i+n})$$

这个优化方法用的比较多，计算效率高且收敛稳定，是现在深度学习的主流方法。当使用小批量样本来估计梯度时，由于估计的梯度往往会偏离真实的梯度，这可以视作在学习的过程中加入了噪声扰动，这种扰动会带来一些正则化的效果。
batch size越大，则小批量样本估计总体梯度约可靠，则每次参数更新沿总体梯度的负方向的概率越大。但是，训练误差收敛速度快，并不意味着模型的泛化性能强，此时的噪声太小，不足以将参数推出尖锐极小值的吸引区域。解决方案是：提高学习率，从而放大梯度噪声的贡献。
上面的方法都存在一个问题，就是update更新的方向完全依赖计算出来的梯度，很容易陷入局部最优的马鞍点。能不能改变其走向，又保证原本的梯度方向，就像向量变换一样，我们模拟物理中物体流动的动量概念（惯性），引入Momentum的概念。

2. Momentum

在更新方向的时候保留之前的方向，增加稳定性而且还有摆脱局部最优的能力。

$$\Delta w=\alpha \Delta w- \eta \bigtriangledown L(w)$$ $$w=w+\Delta w$$

若当前梯度的方向与历史梯度方向一致（表明当前样本不太可能为异常点），则会增强这个方向的梯度，若当前梯度与历史梯度方向不一致，则梯度会衰减。一种形象的解释是：我们把一个球推下山，球在下坡时积聚动量，在途中变得越来越快，$\eta$可视为空气阻力，若球的方向发生变化，则动量会衰减。

3. Adagrad

Adagrad(adaptive gradient)自适应梯度算法，是一种改进的随机梯度下降算法。以前的算法中，每一个参数都使用相同的学习率$\alpha$,而Adagrad算法能够在训练中自动对learning_rate进行调整，出现频率较低参数采用较大的$\alpha$更新，出现频率较高的参数采用较小的$\alpha$更新，根据描述这个优化方法很适合处理稀疏数据。

$$G=\sum ^{t}_{\tau=1}g_{\tau} g_{\tau}^{T} \quad s.t. \ g_{\tau}=\bigtriangledown L(w_{i})$$ $$G_{j,j}=\sum _{\tau=1}^{t} g_{\tau,j\cdot}^{2}$$

这个对角线矩阵的元素代表的是参数的出现频率，每个参数的更新：

$$w_{j}=w_{j}-\frac{\eta}{\sqrt{G_{j,j}}}g_{j}$$

4. RMSprop

RMSprop(root mean square propagation)也是一种自适应学习率方法，不同之处在于，Adagrad会累加之前所有的梯度平方，RMSprop仅仅是计算对应的平均值，可以缓解Adagrad算法学习率下降较快的问题。

$$v(w,t)=\gamma v(w,t-1)+(1-\gamma)(\bigtriangledown L(w_{i}))^{2}$$

其中 $\gamma$ 是遗忘因子

参数更新

$$w=w-\frac{\eta}{\sqrt{v(w,t)}}\bigtriangledown L(w_{i})$$

5. Adam

Adam(adaptive moment estimation)是对RMSprop优化器的更新，利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。优点：每一次迭代学习率都有一个明确的范围，使得参数变化很平稳。Adam记录梯度的一阶矩（first moment），即过往梯度与当前梯度的平均，这体现了惯性保持；另一方面，Adam还记录梯度的二阶矩（second moment），即过往梯度平方与当前梯度平方的平均，这类似AdaGrad方法，为不同参数产生自适应的学习速率。

$$m_{w}^{t+1}=\beta_{1}m_{w}^{t}+(1-\beta_{1}) \bigtriangledown L^{t}$$ $$v_{w}^{t+1}=\beta_{2}m_{w}^{t}+(1-\beta_{2}) (\bigtriangledown L^{t})^{2}$$

其中，m为一阶矩估计，v为二阶矩估计，然后进行估计校正，实现无偏估计

$$\hat{m}_{w}=\frac{m_{w}^{t+1}}{1-\beta_{1}^{t+1}}$$ $$\hat{v}_{w}=\frac{v_{w}^{t+1}}{1-\beta_{2}^{t+1}}$$ $$w^{t+1} \leftarrow=w^{t}-\eta \frac{\hat{m}_{w}}{\sqrt{\hat{v}_{w}}+\epsilon}$$

拟牛顿法

牛顿法的基本思想是在现有极小点估计值的附近对$f(x)$做二阶泰勒展开，进而找到极小点的一个估计值。这个方法需要目标函数是二阶连续可微的。由于牛顿法中需要求解二阶偏导，这个计算量会比较大，而且又是目标函数求出的海森矩阵无法保持正定，因此提出了拟牛顿法。拟牛顿法是一些算法的总称，它们的目的是通过某种方式来近似表示海森矩阵（或者它的逆矩阵）。和牛顿法的区别是，它在更新参数$w$之后更新一下近似海森矩阵的值，而牛顿法是在更新$w$之前完全的计算一遍海森矩阵。
梯度下降和拟牛顿法的异同？
1）参数更新模式相同。
2）梯度下降法利用误差的梯度来更新参数，拟牛顿法利用海森矩阵的近似来更新参数。
3）梯度下降是泰勒级数的一阶展开，而拟牛顿法是泰勒级数的二阶展开。
4）SGD能保证收敛，但是L-BFGS在非凸时不收敛。

Batch Size

在合理的范围内，增大batch size的好处

1）内存利用率提高了，大矩阵乘法的并行化效率提高
2）跑完一次epoch所需的迭代次数减少，对于相同数据量的处理速度进一步加快。
3）在一定范围内，一般来说batch size越大，其确定的下降方向越准，引起训练振荡越小。

盲目增大batch size的坏处

1）内存利用率提高，但是内存容量可能撑不住
2）跑完一次epoch所需的迭代次数减少，要想达到相同的精度，其所花费的时间大大增加，从而对参数的修正也就显得更加缓慢。
3）batch size增大到一定程度，其确定的下降方向已经基本不再改变。

调节batch size对训练效果的影响

1）batch size太小，模型表现效果很差（error增大）
2）随着batch size增大，处理相同数据量的速度越快
3）随着batch size增大，达到相同精度所需的epoch数量越多。
4）由于上述两种因素的矛盾，batch size增大到某个时候，达到时间上的最优。
5）由于最终收敛精度会陷入不同的局部极值，因此batch size增大到某些时候，达到最终收敛精度上的最优。

L1、L2范数

在机器学习中几乎可以看到在损失函数后面都会添加一个额外项，常用的额外项一般有两种，称为L1正则化和L2正则化，或者L1范数和L2范数。L1范数和L2范数可以看做是损失函数的惩罚项，所谓“惩罚”是指对损失函数中的某些参数做些限制。对于现在的回归模型，使用L1范数的模型叫做Lasso回归，使用L2范数的模型叫做Ridge回归（岭回归）。

L1范数

L1范数是指向量中各个元素绝对值之和，也叫“稀疏规则算子”(Lasso regularization)。稀疏的意思是可以让权重矩阵的一部分值等于0。为什么L1范数会使权值稀疏？有一种回答“它是L0范数的最优凸近似”，还存在一种更优雅的回答：任何的规则算子，如果他在$w_{i}=0$处不可微，并且可以分解为一个“求和”的形式，那么这个规则化算子可以实现稀疏。

$$||x||_{1}=\sum_{i}|x_{i}|$$

L1范数可以实现稀疏，而实现稀疏的作用为：
1) 可解释性：可以看到到底是哪些特征和预测的信息有关
2) 特征选择：输入的x的大部分特征与输出y是没有关系的，如果让参数矩阵w中出现许多0，则可以直接干掉与y无关的元素，也就是选择出于y真正相关的特征。如果不这么做，那么x中本来与y无关的特征也加入到模型中，虽然会更好的减小训练误差，但是在预测新样本时会考虑到无关的信息，干扰了预测。

L2范数

L2范数是指向量中各元素的平方和然后再求平方根，也叫做“岭回归(Ridge Regression)”，或叫做“权值衰减(weight decay)”。

$$||x||_{2}=\sqrt{\sum_{i}x_{i}^2}$$

L2范数与L1范数不同，它不会让参数等于0，而是让每个参数都接近于0。L2范数的优点是：
1) 防止过拟合。一般的用法是在损失函数后面加上w的L2范数，即$||x||_{2}$，这是一种规则。
2) 优化求解变得稳定快速。简单地说它可以让$w$在接近全局最优点$w^*$的时候，还保持较大的梯度。这样可以跳出局部最优，也使得收敛速度变快。

L1和L2正则分别有什么特点？为何L1稀疏？

L1范数对异常值更鲁棒，在0点不可导计算不方便，且没有唯一解，L1范数输出稀疏，会把不重要的特征值置0。
L2范数计算方便，对异常值敏感，且有唯一解。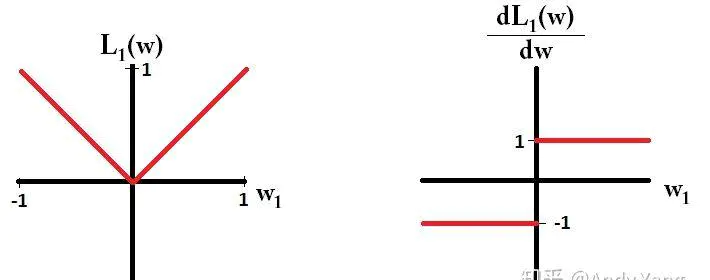

加入L1正则项后，对带正则项的目标函数求导，正则项部分产生的导数在原点左边部分是−C，在原点右边部分是C，因此，只要原目标函数的导数绝对值小于C，那么带正则项的目标函数在原点左边部分始
终是递减的，在原点右边部分始终是递增的，最小值点自然在原点处。相反，L2正则项在原点处的导数是0，只要原目标函数在原点处的导数不为0，那么最小值点就不会在原点，所以L2只有减小w绝对值的作用，对解空间的稀疏性没有贡献。

L1不可导的时候该怎么办

当损失函数不可导，梯度下降不再有效，可以使用坐标轴下降法。梯度下降是沿着当前点的负梯度方向进行参数更新，而坐标轴下降法是沿着坐标轴的方向。假设有m个特征个数，坐标轴下降法进行参数更新的时候，先固定m-1个值，然后再求另外一个的局部最优解，从而避免损失函数不可导问题。坐标轴下降法每轮迭代都需要O(mn)的计算，和梯度下降算法相同。

激活函数

神经网络的每个神经元接受上一层神经元的输出值作为本神经元的输入值，并将输入值传递给下一层，输入神经元节点会将输入属性值直接传递给下一层（隐藏层或输出层）。上层函数的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数。如果不用激活函数，在这种情况下每一层节点的输入都是上一层输出的线性函数，很容易验证，无论神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，这种情况就是最原始的感知机（Perceptron），那么网络的逼近能力就相当有限。我们引入非线性函数作为激励函数，这样深层神经网络表达能力就更加强大，几乎可以逼近任意函数。

Sigmoid函数

Signoid是常用的非线性的激活函数，它的数学形式如下：

$$f(z)=\frac{1}{1+e^{-z}}$$

其导数为：

$$\frac{df}{dz}=f(z)(1-f(z))$$

Sigmoid的几何如下：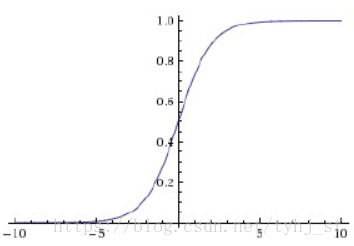

特点：它能够把输入的连续实值变换为0和1之间的输出，对于非常大的负数则输出为0，非常大的正数则输出为1.
缺点：
1) 在深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失，其中梯度爆炸发生的概率非常小，而梯度消失发生的概率比较大。Sigmoid函数的倒数如下所示：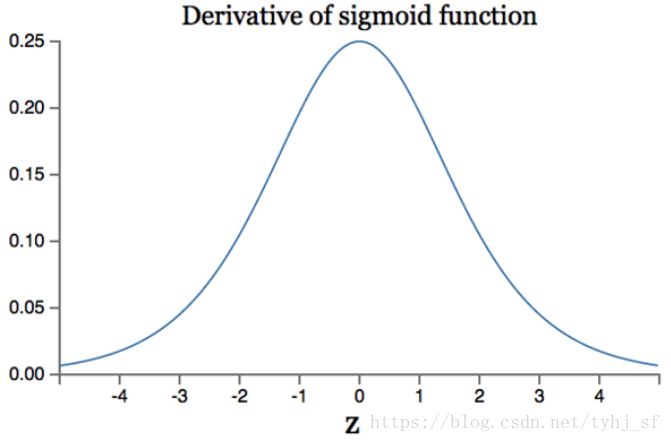

如果我们初始化神经网络的权值为[0,1]之间的随机值，由反向传播算法的数学推导可知，梯度从后向前传播时，每传递一层梯度值都会减少为原来的0.25倍，如果神经网络隐藏层特别多时，那么梯度在多层传递之后就变得非常小接近于0，即出现梯度消失现象；当网络权值初始化为$(1,+\infty)$区间的值，则会出现梯度爆炸情况。
2) Sigmoid的输出不是0均值，这会导致后一层的神经元将上一层的神经元输出的非0均值的信号作为输入。产生的结果是：如果$x>0, f=w^Tx+b$，那么对$w$求局部梯度则都为正，这样反向传播的过程中$w$要么都向正方向更新，要么都往负方向更新，使得收敛缓慢。当然，如果按batch训练，那么那个batch可能会得到不同的信号，这个问题可以缓解一下。非0均值问题虽然会产生一些不好的影响，不过跟梯度消失问题相比还是要好很多。
3) 其解析式中含有幂运算，计算求解时相对比较耗时。对于规模较大的深度网络，这回较大地增加训练时间。

tanh函数

tanh函数的解析式：

$$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

其导数为：

$$tanh'(x)=1-tanh^2(x)$$

tanh函数及其导数的几何图像如下：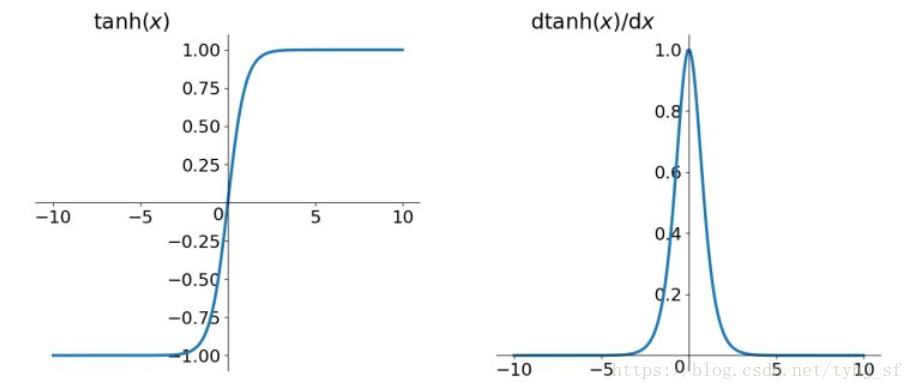

tanh函数解决了Sigmoid函数不是zero-centered输出的问题，然而，梯度消失的问题和幂运算的问题仍然存在。

Relu函数

Relu函数的解析式：

$$Relu=max(0, x)$$

Relu函数及其导数的图像如下图所示：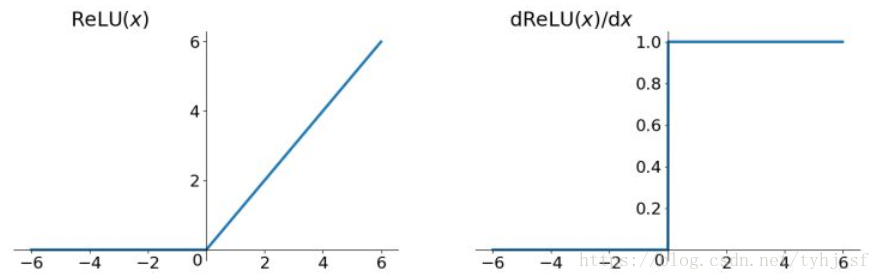

ReLU其实是一个取最大值函数，注意这并不是全区间可导的，但是我们可以取sub-gradient，如上图所示。
优点：1）解决了梯度消失问题(gradient vanishing)问题（在正区间）。 2）计算速度非常快，只需要判断输入是否大于0。 3）收敛速度远快于sigmoid和tanh函数。
ReLU也有几个需要注意的问题：
1) ReLU的输出不是zero-centered。
2) Dead ReLU Problem，指的是某些神经元可能永远不会被激活，导致相应的参数永远不会被更新。有两个主要原因可能会导致这种情况：参数的初始化或learning_rate太大导致训练过程中参数更新太大进入这种状态。
解决的方法是采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。Xavier初始化方法是一种很有效的神经网络初始化方法，为了使得网络中信息更好的流动，每一层输出的方法应该尽量相等。

Leaky ReLU函数

函数表达式：

$$f(x)=max(\alpha x, x)$$

Leaky Relu函数及其导数的图像如下图所示：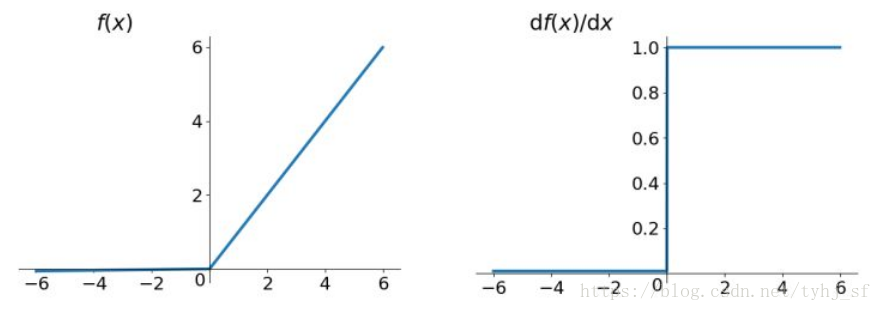

图中左半边直线斜率非常接近于0，所以看起来像是平的。为了解决Dead ReLU Problem，通过将ReLU的前半段设为$\alpha x$而不是0，通常$\alpha =0.01$。理论上讲，Leaky ReLU有ReLU的所有优点，外加不会有Dead ReLU问题，但在实际操作中，并没有完全证明Leaky ReLU总是好于ReLU。

ELU函数

函数表达式为：

$$f(x)= \begin{cases} x &\text(if\ x>0)\\ \alpha(e^x-1) &\text{otherwise} \end{cases}$$

函数及其导数的图像如下：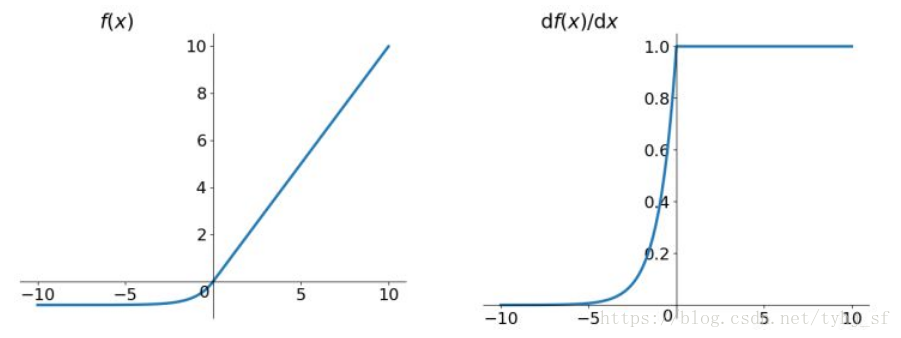

显然，ELU有ReLU的基本所有优点，以及不会有Dead ReLU问题，输出的均值接近于0，是zero-centered。它的一个小问题在于计算量稍大。

神经网络权重初始化方式

在深度学习找那个，神经网络的权重初始化方法(weight initialization)对模型的收敛速度和性能有着至关重要的影响。神经网络其实就是对权重参数w的不停迭代更新，以期达到较好的性能。在深度神经网络中，随着层数的增多，在梯度下降的过程中，极易出现梯度消失或者梯度爆炸。因此，对权重w的初始化显得至关重要，一个好的权重初始化虽然不能完全解决梯度消失和梯度爆炸问题，但是对于处理这两个问题是由很大的帮助的，并且十分有利于模型性能和收敛速度。

初始化为0

在线性回归和logistics回归中可以使用，因为隐藏层只有一层。在超过一层的神经网络中就不能够使用了。因为如果所有的权重参数都为0，那么所有的神经元输出都是一样的，在反向传播时向后传递的梯度也是一致，将无法发挥多层的效果，实际上相当于一层隐藏层。

随机初始化

卷积层的方差为：

$$Var(w_ix_i)=E[w_i]^2Var(x_i)+E[x_i]^2Var(w_i)+Var(w_i)Var(x_i)$$

使用高斯随机初始化时要把W随机初始化到一个相对较小的值，因为如果X很大的话，W又相对较大，会导致输出值特别大，这样如果激活函数是sigmoid，就会导致sigmoid的输出值为1或0，导致更多的问题。但是随机初始化也有缺点，在均值为0，方差为1的高斯分布中，当神经网络层数增加时，会发现越往高层的激活函数（tanh函数）的输出值几乎都接近于0，使得神经元不被激活。

Xavier初始化

每层的权重初始化为：

$$W\sim U[-\frac{\sqrt{6}}{\sqrt{n_j+n_{j+1}}}, \frac{\sqrt{6}}{\sqrt{n_j+n_{j+1}}}]$$

服从均匀分布，$nj$为输入层的参数，$n{j+1}$为输出层参数。
Xavier是为了解决随机初始化问题而提出的一种初始化方式，其思想是尽可能让输入和输出服从相同的分布，这样能够避免高层的激活函数的输出值趋向于0。虽然Xavier初始化能很好地用于tanh函数，但是对于目前最常用的ReLU激活函数，还是无能为力，因此引出He initialization。

MSRA/He initialization

Xavier初始化对于Relu激活函数表现非常不好，因此何恺明针对ReLU重新推导，每层的初始化公式为：

$$W\sim U[0, \sqrt{\frac{2}{n}}]$$

是一个均值为0，方差为$\frac{2}{n}$的高斯分布。
缺点是：MSRA方法只考虑一个方向，无法使得正向反向传播时方差变化都很小。

损失函数

损失函数、代价函数与目标函数

损失函数(Loss Function)：是定义在单个样本上的，是指一个样本的误差。
代价函数(Cost Function)：是定义在整个训练集上，是所有样本误差的平均值，也就是所有损失函数值的平均。
目标函数(Object Function)：是指最终需要优化的函数，一般来说是代价函数+正则化项。

常用的损失函数

（1）0-1损失函数(0-1 loss function)

$$L(y, f(x))= \begin{cases} 1, &\text{y}\ne\text{f(x)}\\ 0, &\text{y}=\text{f(x)} \end{cases}$$

即，当预测错误时，损失函数为1，当预测正确时，损失函数值为0.该损失函数不考虑预测值与真实值之间的误差程度。
（2）平方损失函数（quadratic loss function）

$$L(y,f(x))=(y-f(x))^2$$

是指预测值与实际值差的平方。
（3）绝对值损失函数（absolute loss function）

$$L(y,f(x))=|y-f(x)|$$

该损失函数只是取了绝对值而不是求平方值，差距不会被平方放大。
（4）对数损失函数(logarithmic loss function)

$$L(y, p(y|x))=-logp(y|x)$$

该损失函数用到了极大似然估计思想。P(Y|X)通俗的解释是：在当前模型的基础上，对于样本X，其预测值为Y，也就是预测正确的概率。由于概率之间同时满足需要使用乘法，为了将其转化为加法，我们将其取对数。最后由于是损失函数，所以预测正确的概率越高，其损失值应该越小，因此再加个符号取反。
（5）Hinge loss
Hinge loss一般分类算法中的损失函数，尤其是SVM，其定义为：

$$L(w,b)=max(0, 1-yf(x))$$

其中$y=+1$或$y=-1$，$f(x)=wx+b$，当为SVM的线性核时。

常用的代价函数

（1）均方误差(Mean Squared Error)

$$MSE=\frac{1}{N}\sum_{i=1}^N(y^{(i)}-f(x^{(i)}))^2$$

均方误差是指参数估计值与真实值之差的平方的期望值，MSE可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精度。（i表示第i个样本，N表示样本总数）。
通常用来做回归问题的代价函数。
（2）均方根误差

$$RMSE=\sqrt{\frac{1}{N}\sum_{i=1}^N(y^{(i)}-f(x^{(i)}))^2}$$

均方根误差是均方误差的算术平方根，能够直观观测预测值与真实值的离散程度。通常用来作为回归算法的性能指标。
（3）平均绝对误差（Mean Absolute Error）

$$MAE=\frac{1}{N}\sum_{i=1}^N|y^{(i)}-f(x^{(i)})|$$

平均绝对误差是绝对误差的平均值，平均绝对误差能更好地反映预测值误差的实际情况。通常用来作为回归算法的性能指标。
（4）交叉熵代价函数(Cross Entry)

$$H(p,q)=-\frac{1}{N}\sum_{i=1}^Np(x^{(i)})log(x^{(-i)})$$

交叉熵是用来评估当前训练得到的概率分布于真实分布的差异情况，减少交叉熵损失就是在提高模型的预测准确率。其中p(x)是指真实分布的概率，q(x)是模型通过数据计算出来的概率估计。
对于二分类模型的交叉熵代价函数：

$$L(w,b)=-\frac{1}{N}\sum_{i=1}^N(y^{(i)}logf(x^{(i)})+(1-y^{(i)})log(1-f(x^{(i)})))$$

其中f(x)可以是sigmoid函数或深度学习中的其他激活函数，而$y{(i)}\in 0,1$。
交叉熵通常用作分类问题的代价函数。
常用损失函数

为什么分类问题用 cross entropy，而回归问题用 MSE?

优秀解答
当sigmoid函数和MSE一起使用时会出现梯度消失。原因如下：
1）MSE对参数w,b的偏导，其中预测值为a，真实值为y，则$z=wx+b$，$a=\sigma(z)$，$\sigma$是sigmoid函数，损失函数$J=(y-a)^2$。

$$\frac{\partial J}{\partial w}=(a-y)\sigma(z)'x$$ $$\frac{\partial J}{\partial b}=(a-y)\sigma(z)'$$

2）cross-entry对参数的偏导

$$\frac{\partial J}{\partial w}=\frac{1}{n}\sum(a-y)x$$ $$\frac{\partial J}{\partial b}=\frac{1}{n}\sum(a-y)$$

使用MSE时，w、b的梯度均与sigmoid函数对z的偏导有关系，而sigmoid函数的偏导在自变量非常大或者非常小时，偏导数的值接近于零，这将导致w、b的梯度将不会变化，也就是出现所谓的梯度消失现象。而使用cross-entropy时，w、b的梯度就不会出现上述的情况。
当MSE和交叉熵同时应用到多分类场景下时，（标签的值为1时表示属于此分类，标签值为0时表示不属于此分类），MSE对于每一个输出的结果都非常看重，而交叉熵只对正确分类的结果看重。交叉熵的损失函数只和分类正确的预测结果有关系，而MSE的损失函数还和错误的分类有关系，该分类函数除了让正确的分类尽量变大，还会让错误的分类变得平均，但实际在分类问题中这个调整是没有必要的。但是对于回归问题来说，这样的考虑就显得很重要了。所以，回归问题熵使用交叉熵并不合适。

Batch Normalization

BN归纳
Batch Normalization就是在训练过程中使得每一层神经网络的输入保持相同分布的。BN的基本思想相当直观：随着网络深度加深或者在训练过程中，神经元的输入值分布逐渐发生偏移或变动，使得整体分布逐渐往非线性函数的取值区域的上下限两端靠近，所以这导致反向传播时低层神经网络的梯度消失，这是训练深层神经网络收敛越来越慢的本质原因。而BN就是通过一定的规范化手段，把该层任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布，其实就是把越来越偏的分布强制拉回到标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就是导致损失函数较大的变化，使得梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。
如果都通过BN，那么不就跟把非线性函数替换成线性函数效果相同吗？这意味着什么？我们知道，如果是多层的线性函数变换其实这个深层网络就没有意义，因为多层线性网络跟一层线性网络是等价的。这意味着网络的表达能力又下降了。所以BN为了保证非线性的获得，对变换后的满足均值为0方差为1的$x$又进行了scale加上shift操作($y=scale*x+shift$)，每个神经元增加了两个参数scale和shift参数，这两个参数是通过训练学习到的，意思是通过scale和shift把输入值从标准正太分布左移或右移一点并拉伸或缩短一点，每个实例的挪动情况不一样，来找到一个线性和非线性的较好平衡点，使得既能享受非线性的较强表达能力的好处，又避免太靠近非线性区两头使得网络的收敛速度太慢。
BatchNorm在网络中的作用：BN层添加在激活函数前，对输入激活函数的输入进行归一化，这样解决了输入数据发生偏移和增大的影响。

BatchNorm的优缺点

优点：1）极大提升了训练速度，使得收敛过程大大加快；2）还能增加分类效果，一种解释是这类似于Dropout的一种防止过拟合的正则化表达方式，所以不用Dropout也能达到相当的效果；3）调参过程也简单了，对于初始化要求没那么高，可以使用大的学习率。
缺点：1）高度依赖于batch size的大小，它要求batch size都比较大，因此不适合batch size较小的场景。2）不适合RNN网络，因为不同样本的长度不同，RNN的深度是不固定的。同一个batch中多个样本会产生不同深度的RNN，因此很难对同一层的样本进行归一化。

BN的计算流程

首先，对(B,W,H)通道计算样本的均值和方差，将样本数据进行标准化处理，然后引入$\gamma$和$\beta$两个参数进行平移和缩放处理，让网络可以学习恢复出原始网络所要学习的特征分布。

BN的训练和测试

对于BN，在训练时，是对每一批的训练数据进行归一化，也即用每一批数据的均值和方差。
而在测试时，比如进行一个样本的预测，就并没有batch的概念，因此，这个时候用的均值和方差是全量训练数据的均值和方差，这个可以通过移动平均法求得。
BN训练时为什么不用全量训练集的均值和方差呢？
因为用全量训练集的均值和方差容易过拟合，对于BN，其实就是对每一批数据进行归一化到一个相同的分布，而每一批数据的均值和方差会有一定的差别，而不是用固定的值，这个差别实际上能够增加模型的鲁棒性，也会在一定程度上减少过拟合。

Dropout

Dropout指的是让这些神经元失效或者状态抑制，可以防止参数过分依赖训练数据，增加参数对数据集的泛化能力。
在训练阶段，Dropout通过在每次迭代中随机丢弃一些神经元来改变网络的结构，以实现训练不同结构的神经网络的目的；而在测试阶段，Dropout则会使用全部的神经元，这相当于之前训练的不同结构的网络全都参与对最终结果的投票，以获得较好的效果。Dropout通过这种方式提供了一种强大、快捷且易实现的近似Bagging方法。需要注意的是，在原始的Bag个ing中所有模型是相互独立的，而Dropout则有所不同，这里不同的网络其实是共享了参数的。
另一方面，Dropout能够减少神经元之间复杂的共适应关系。由于Dropout每次丢弃的神经元是随机选择的，所以每次保留下来的网络会包含不同的神经元，这样在训练过程中，网络权值的更新不会依赖于隐节点之间的固定关系（固定关系可能会产生一些共同作用从而影响网络的学习过程）。换句话说，网络中每个神经元不会对另一个特定神经元的激活非常敏感，这使得网络能够学习到一些更加泛化的特征。

Dropout 在训练和测试时都需要嘛？

Dropout 在训练时采用，是为了减少神经元对部分上层神经元的依赖，类似将多个不同网络结构的模型集成起来，减少过拟合的风险。
而在测试时，应该用整个训练好的模型，因此不需要dropout。

Dropout 如何平衡训练和测试时的差异呢？

Dropout ，在训练时以一定的概率使神经元失活，实际上就是让对应神经元的输出为0
假设失活概率为 p ，就是这一层中的每个神经元都有p的概率失活，如下图的三层网络结构中，如果失活概率为0.5，则平均每一次训练有3个神经元失活，所以输出层每个神经元只有3个输入，而实际测试时是不会有dropout的，输出层每个神经元都有6个输入，这样在训练和测试时，输出层每个神经元的输入和的期望会有量级上的差异。
因此在训练时还要对第二层的输出数据除以（1-p）之后再传给输出层神经元，作为神经元失活的补偿，以使得在训练时和测试时每一层输入有大致相同的期望。

在循环神经网络中如何使用Dropout？

Dropout方法会在训练过程中将网络中的神经元随机丢弃，然而循环神经网络具有记忆功能，其神经元的状态包含了之前时刻的状态信息，如果直接用Dropout删除一些神经元，会导致循环神经网络的记忆力减退。另外，有实验表明，如果循环神经网络不同时刻间的连接层中加入噪声，则噪声会随着序列长度的增加而不断放大，并最终淹没重要的信号信息。
在循环神经网络中，连接层可以分成两种类型：一种是从t时刻的输入一直到t时刻的输出之间的连接，称为前馈连接；另一种是从t时刻到t+1时刻之间的连接，称为循环连接。如果要将Dropout用在循环神经网络上，一个较为直观的思路就是，只将Dropout用在前馈连接上，而不用在循环连接上。注意，这里Dropout随机丢弃的是连接，而不是神经元。
然而，只在前馈连接中应用Dropout对于过拟合问题的缓解效果并不太理想，这是因为循环神经网络中大量参数其实是在循环连接中。因此，论文提出基于变分推理的Dropout方法，即对于同一个序列，在其所有时刻的循环连接上采用相同的丢弃方法，也就是说不同时刻丢弃的连接是相同的。实验结果表明，这种Dropout在语言模型和情感分析中会获得较好的效果。

深度学习几种归一化（BN、LN、IN、GN）

BN、LN、IN和GN这四个归一化的计算流程几乎是一样的，可以分为四步：1）计算出均值；2）计算出方差；3）归一化处理到均值为0，方差为1；4）变化重构，恢复出这一层网络所要学到的分布。
我们先用一个示意图来形象的表现BN、LN、IN和GN的区别，在输入图片的维度为（NCHW）中，HW是被合成一个维度，这个是方便画出示意图，C和N各占一个维度。

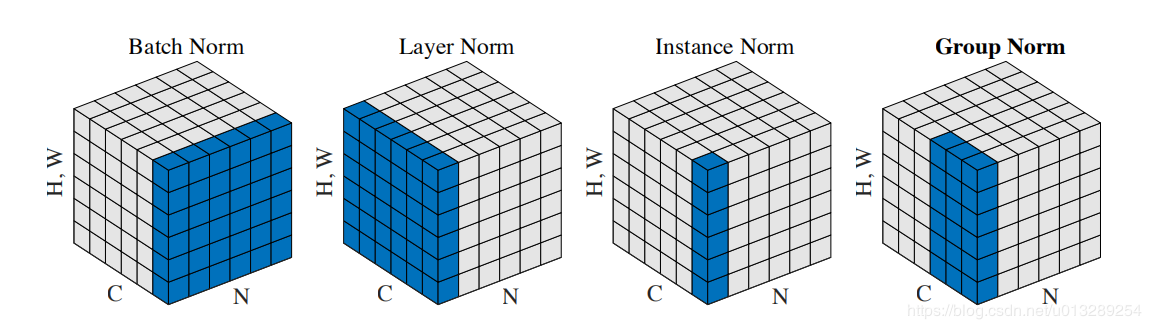
Batch Normalization：
1)BN的计算就是把每个通道的NHW单独拿出来归一化处理
2)针对每个channel我们都有一组γ,β，所以可学习的参数为2*C
3)当batch size越小，BN的表现效果也越不好，因为计算过程中所得到的均值和方差不能代表全局。
Layer Normalizaiton：
1)LN的计算就是把每个CHW单独拿出来归一化处理，不受batchsize 的影响
2)常用在RNN网络，但如果输入的特征区别很大，那么就不建议使用它做归一化处理
Instance Normalization:
1)IN的计算就是把每个HW单独拿出来归一化处理，不受通道和batchsize 的影响。
2)常用在风格化迁移，IN的效果优于BN，因为在这类生成式方法中，每张图片自己的风格比较独立，不应该与batch中其他图片产生太大联系。但如果特征图可以用到通道之间的相关性，那么就不建议使用它做归一化处理。
Group Normalization:
1)GN的计算就是把先把通道C分成G组，然后把每个gHW单独拿出来归一化处理，最后把G组归一化之后的数据合并成CHW。
2)GN介于LN和IN之间，当然可以说LN和IN就是GN的特列，比如G的大小为1或者为C。

解决模型欠拟合与过拟合常用方法

欠拟合

欠拟合：欠拟合的原因大多是模型不够复杂、拟合函数的能力不够。
因此，从数据层面考虑，可以增加新特征，例如：组合、泛化、相关性、高次特征等；从模型层面考虑，可以增加模型的复杂度，例如SVM的核函数、DNN等更复杂模型，去掉正则化或减少正则化参数，加深训练轮数等。

过拟合

过拟合：成因是给定的数据集相对过于简单，使得模型在拟合函数时过分考虑了噪声等不必要的数据间关联。
解决方法：
1）数据扩增：人为增加数据量，可以用重采样、上采样、增加随机噪声、GAN、图像数据的空间变换（平移旋转镜像）、尺度变换（缩放裁剪）、颜色变换、改变分辨率、对比度、亮度等。
2）针对神经网络，采用dropout的方法：dropout的思想是当一组参数经过某一层神经元的时候，去掉这一层上的部分神经元，让参数只经过一部分神经元进行计算。这里的去掉不是真正意义上的去除，只是让参数不经过一部分神经元计算，从而减少了神经网络的规模（深度）。
3）提前停止训练
也就是减少训练的迭代次数。从上面的误差率曲线图，理论上可以找到有个训练程度，此时验证集误差率最低，视为拟合效果最好的点。
4）正则化
在所定义的损失函数后面加入一项永不为0的部分，那么经过不断优化损失函数还是会存在的。
L0正则化：损失函数后面加入L0范数，也就是权重向量中非零参数的个数。特点是可以实现参数的稀疏性，使尽可能多的参数都为0；缺点是在优化时是NP难问题，很难优化。
L1正则化：在损失函数后面加入权重向量的L1范数。L1范数是L0范数的最优凸近似，比L0范数容易优化，也可以很好地实现参数稀疏性。
L2正则化：在损失函数后面加入参数L2范数的平方项。与L0、L1不同的是，L2很难使某些参数达到0，它只能是参数接近0。
5）针对DNN，采用batch normalization：即BN，既能提高泛化能力，又大大提高训练速度，现被广泛应用于DNN的激活层之前。主要优势：减少了梯度对参数大小和初始值的依赖，将参数值（特征）缩放在[0,1]区间（若针对Relu还限制了输出的范围），这样反向传播时梯度控制在1左右，使得网络在较高的学习率之下也不易发生梯度爆炸或弥散（也防止了在使用sigmoid作为激活函数时训练容易陷入梯度极小饱和或极大的极端情况）。

多分类问题

one vs rest

由于概率函数$h_{\theta}(x)$所表示的是样本标记为某一类型的概率，但可以将一对一（二分类）扩展为一对多(one vs rest)：
1）将类型$class_1$看作正样本，其他类型全部看作负样本，然后我们就可以得到样本类型为该类型的概率$p_1$；
2）然后再讲另外类型$class_2$看作正样本，其他类型全部看作负样本，同理得到$p_2$；
3）以此循环，我们可以得到该待预测样本的标记类型分别为类型$class_i$时的概率$p_i$，最后我们取$p_i$中最大的那个概率对应的样本标记类型为我们的待预测样本类型。

softmax函数

使用softmax函数构造模型解决多分类问题，与logistic回归不同的是，softmax回归分类模型会有多个的输出，且输出个数与类别个数相等，输出为样本$X$的各个类别的概率，最后对样本进行预测的类型为概率最高的那个类别。

反向传播原理

反向传播过程：将训练集的数据输入到神经网络的输入层，经过隐藏层最终到达输出层输出结果，这是神经网络的前向传播过程；由于神经网络的输出结果和实际结果存在误差，计算估计值和实际值之间的误差，并将误差从输出层向隐藏层反向传播，直至传播至输入层；在反向传播过程中，根据误差调整各种参数的值，不断迭代上述的过程，直至收敛。
推导过程

什么是梯度消失和梯度爆炸

在反向传播过程中需要对激活函数进行求导，如果导数大于1，那么随着网络层数的增加梯度更新将会朝着指数爆炸的方式增加这就是梯度爆炸。同样如果导数小于1，那么随着网络层数的增加梯度更新信息会朝着指数衰减的方式减少这就是梯度消失。因此，梯度消失、爆炸，其根本原因在于反向传播训练法则，属于先天不足。

梯度消失的原因

1）在反向传播过程中梯度呈指数衰减，随着网络层数的加深，梯度减小为0；2）在反向传播过程中，神经元的输入值位于激活函数的非线性区域的上下限两端，使得梯度消失。
而梯度爆炸一般出现在深层网络和权值初始化太大的情况下。

梯度消失解决方案

1）预训练加微调
2）添加正则项
3）使用relu、leakrelu、elu等激活函数
4）使用batch normalization
5）使用残差结构
6）使用LSTM

性能指标

召回率、精确率、准确率

精确率是针对预测结果而言的，它表示的是预测为正的样本中有多少是真正的正样本。那么预测为正就有两种可能，一种是把正类预测为正类（TP），另一种就是把负类预测为正类（FP），也就是：

$$P=\frac{TP}{TP+FP}$$

而召回率是针对原来的样本而言，它表示的是样本中的正例有多少被预测正确，也有两种可能，一种是把原来的正类预测成正类（TP），另一种就是把原来的正类预测为负类（FN）。

$$R=\frac{TP}{TP+FN}$$

准确率就是所有样本中预测出正例的概率。

$$A=\frac{TP+TN}{TP+FN+FP+TN}$$

Accuracy的局限性

当正负样本极度不均衡时存在问题！比如，正样本有99%时，分类器只要将所有样本划分为正样本就可以达到99%的准确率。但显然这个分类器是存在问题的。当正负样本不均衡时，常用的评价指标为ROC曲线和PR曲线。

ROC曲线和PR曲线

定义真正例率（True Positive Rate）为：$TPR=\frac{TP}{TP+FN}$，其刻画真正的正类中，有多少样本预测为正类的概率。定义假正例率（False Positive Rate）为：$FPR=\frac{FP}{TN+FP}$，其刻画了真正的负类中，有多少样本被预测为正类的概率。以真正例率为纵轴、假正例率为横轴作图，就得到ROC曲线。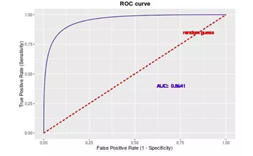

具体方法是在不同的分类阈值 (threshold) 设定下分别以TPR和FPR为纵、横轴作图。曲线越靠近左上角，意味着越多的正例优先于负例，模型的整体表现也就越好。
优点:1）兼顾正例和负例的权衡。因为TPR聚焦于正例，FPR聚焦于负例，使其成为一个比较均衡的评估方法。2）ROC曲线选用的两个指标， TPR和FPR，都不依赖于具体的类别分布。
缺点:1）ROC曲线的优点是不会随着类别分布的改变而改变，但这在某种程度上也是其缺点。因为负例N增加了很多，而曲线却没变，这等于产生了大量FP。像信息检索中如果主要关心正例的预测准确性的话，这就不可接受了。
2）在类别不平衡的背景下，负例的数目众多致使FPR的增长不明显，导致ROC曲线呈现一个过分乐观的效果估计。ROC曲线的横轴采用FPR，根据公式 ，当负例N的数量远超正例P时，FP的大幅增长只能换来FPR的微小改变。结果是虽然大量负例被错判成正例，在ROC曲线上却无法直观地看出来。（当然也可以只分析ROC曲线左边一小段）
PR曲线以查准率（精确率P）为纵轴，查全率（召回率R）为横轴作图，就得到查准率-查全率曲线，简称P-R曲线。
PR曲线与ROC曲线的相同点是都采用了TPR (Recall)，都可以用AUC来衡量分类器的效果。不同点是ROC曲线使用了FPR，而PR曲线使用了Precision，因此PR曲线的两个指标都聚焦于正例。类别不平衡问题中由于主要关心正例，所以在此情况下PR曲线被广泛认为优于ROC曲线。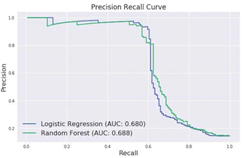

使用场景：
ROC曲线由于兼顾正例与负例，所以适用于评估分类器的整体性能，相比而言PR曲线完全聚焦于正例。
如果有多份数据且存在不同的类别分布，比如信用卡欺诈问题中每个月正例和负例的比例可能都不相同，这时候如果只想单纯地比较分类器的性能且剔除类别分布改变的影响，则ROC曲线比较适合，因为类别分布改变可能使得PR曲线发生变化时好时坏，这种时候难以进行模型比较；反之，如果想测试不同类别分布下对分类器的性能的影响，则PR曲线比较适合。
如果想要评估在相同的类别分布下正例的预测情况，则宜选PR曲线。
类别不平衡问题中，ROC曲线通常会给出一个乐观的效果估计，所以大部分时候还是PR曲线更好。
最后可以根据具体的应用，在曲线上找到最优的点，得到相对应的precision，recall，f1 score等指标，去调整模型的阈值，从而得到一个符合具体应用的模型。

AUC曲线

AUC（Area Under the Curve）可解读为：从所有正例中随机选取一个样本A，再从所有负例中随机选取一个样本B，分类器将A判为正例的概率比将B判为正例的概率大的可能性。
我们最直观的有两种计算AUC的方法：1）绘制ROC曲线，ROC曲线下面的面积就是AUC的值。2）假设总共有（m+n）个样本，其中正样本m个，负样本n个，总共有mn个样本对，计数，正样本预测为正样本的概率值大于负样本预测为正样本的概率值记为1，累加计数，然后除以（mn）就是AUC的值。
AUC指标有什么特点？放缩结果对AUC是否有影响？
AUC（Area under Curve）指的是ROC曲线下的面积，介于0和1之间。AUC作为数值可以直观地评价分类器的好坏，值越大越好。它的统计意义是从所有正样本随机抽取一个正样本，从所有负样本随机抽取一个负样本，当前score使得正样本排在负样本前面的概率。放缩结果对AUC没有影响。

训练集、验证集和测试集

1）通常80%为训练集，20%为测试集。
2）当数据量较小时（万级别及以下）的时候将训练集、验证集以及测试集划分为6：2：2；若是数据很大，可以将训练集、验证集、测试集比例调整为98：1：1。
3）当数据量很小时，可以采用K折交叉验证。K折交叉验证将数据集A随机分为k个子集，每个子集均做一次测试集，其余的作为训练集。交叉验证重复k次，每次选择一个子集作为测试集，并将k次的平均交叉验证识别正确率作为结果。
4）划分数据集时可采用随机划分法（当样本比较均衡时），分层采样法（当样本分布极度不均衡时）。分层抽样是指在抽样时，将总体分成互不相交的层，然后按照一定的比例，从各层独立地抽取一定数量的个体，将各层取出的个体合在一起作为样本的方法。

偏差和方差

偏差：描述预测值的期望与真实值之间的差别，偏差越大说明模型的预测结果越差，刻画了学习算法本身的拟合能力。
方差：描述预测值的变化范围，方差越大说明模型的预测越不稳定，刻画了数据扰动造成的影响。
高方差过拟合，高偏差欠拟合。常用交叉验证来权衡模型的方差和偏差。也可以比较均方误差$MSE=E[(\hat{\theta_m}-\theta)^2]=Bias(\hat{\theta_m})^2+Var(\hat{\theta_m})^2$
给定学习任务：
1)在训练不足时模型的拟合能力不够强，训练数据的扰动不足以使模型产生显著变化，此时偏差主导了泛化误差。
2)随着训练程度的加深模型的拟合能力逐渐增强，训练数据发生的扰动逐渐被模型学习到，方差逐渐主导了泛化误差。
3)在训练充分后模型的拟合能力非常强，训练数据发生的轻微扰动都会导致模型发生显著变化。若训练数据自身的、非全局的特性被模型学到了，则将发生过拟合。

深度模型参数调整的一般方法论

1）学习率：遵循小->大->小原则
2）初始化：选择合适的初始化方式，有预训练模型更好
3）优化器选择：adam比较快，sgd较慢
4）loss：回归问题选L2 loss，分类问题选交叉熵
5）从小数据大模型入手，先过拟合，再增加数据并根据需要调整模型复杂度。
6）可视化

pytorch与tensorflow的区别

创建和运行计算图可能是两个框架最不同的地方。在PyTorch中，图结构是动态的，这意味着图在运行时构建。而在TensorFlow中，图结构是静态的，这意味着图先被“编译”然后再运行。
动态图的还有一个好处就是比较容易调试, 在 PyTorch 中, 代码报错的地方, 往往就是代码错写的地方, 而静态图需要先根据代码生成 Graph 对象, 然后在 session.run() 时报错, 但是这种报错几乎很难直接找到代码中对应的出错段落。
pytorch基础知识

卷积神经网络模型

卷积神经网络

卷积层

卷积层是通过特定数目的卷积核（又称滤波器）对输入的多通道特征图进行扫描和运算，从而得到多个拥有更高层语义信息的输出特征图（通道数等于卷积核个数）。
输入图像的维数通常很高，例如，1000x1000大小的彩色图像对应于三百万维特征。因此，继续沿用多层感知机中全连接层会导致庞大的参数量。大参数量需要繁重的计算，而更重要的是大参数量会有更高的过拟合风险。卷积是局部连接、共享参数的全连接层。这两个特征使参数量大大降低。卷积层中的权值通常被称为滤波器(filter)或卷积核(convolution kernel)。
局部连接：所谓局部连接，就是卷积层的节点仅仅和前一层的部分节点相连接，只用来学习局部特征，而全连接层中，每个输出通过权值(weight)和所有输入相连。在计算机视觉中，图像中的某一块区域中，像素之间的相关性与像素之间的距离同样相关，距离较近的像素之间相关性强，距离较远则相关性比较弱，所以局部相关性理论同样适用于计算机视觉的图像处理领域。在卷积层中，每个输出神经元在通道方向保持全连接，在空间方向上只和上一层一部分输入神经元相连。局部感知采用部分神经元接收图像信息，再通过综合全部的图像信息达到增强图像信息的目的。这种局部连接的方式大大减少了参数数量，加快了学习速率，同时也在一定程度上减少过拟合的可能。
共享参数：如果一组权值可以在图像中某个区域提取出有效的表示，那么它们也能在图像中的另外区域提取出有效的表示。也就是说，如果一个模式(pattern)出现在图像中的某个区域，那么它们也可以出现在图像中的其他任何区域。因此，卷积层不同空间位置的神经元共享权值，用于发现图像中不同空间位置的模式。权值共享其实就是整张图片在使用同一个卷积核内的参数提取特征，但是不同的卷积核提取的是不同特征，因此不同卷积核间的神经元权值是不共享的。卷积层在空间方向共享参数，而循环神经网络在时间方向共享参数。
描述卷积的四个量：一个卷积层的配置由如下四个量确定。1）卷积核个数。使用一个卷积核进行卷积可以得到一个二维的特征图(feature map)。使用多个卷积核进行卷积，可以得到不同特征的feature map。2）感受野（receptive field）F，即卷积核的大小。3）零填充(zero-padding)P，随着卷积的进行，图像的大小将缩小，图像边缘的信息将逐渐丢失，因此在卷积前，我们在图像上下左右填补一些0，使得我们可以控制输出特征图的大小。4）步长(stride)S，卷积核在输入图像上每移动S个位置计算一个输出神经元。
假设输入图片大小为$I\times I$，卷积核大小为$K\times K$，步长为S，填充的像素为P，则卷积层输出的特征图大小为：

$$O=(I-K+2P)/S+1$$

池化层

池化层根据特征图上的局部统计信息进行下采样，在保留有用信息的同时减少特征图的大小。和卷积层不同，池化层不包含需要学习的参数，最大池化层(max-pooling)在一个局部区域选最大值输出，而平均池化(average pooling)计算一个区域的均值作为输出。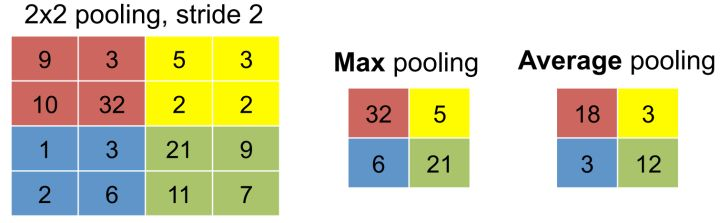

池化层的作用：1）增加特征平移不变性，池化可以提高网络对微小位移的容忍能力。2）减小特征图大小，池化层对空间局部区域进行下采样，使下一层需要的参数量和计算量减少，并降低过拟合风险。3）最大池化可以带来非线性，这是目前最大池化更常使用的原因。
平均池化和最大池化的区别：最大池化保留了纹理特征，平均池化保留整体的数据特征。最大池化提取边缘等“最重要”的特征，而平均池化提取的特征更加smoothly。

全连接层

全连接层（fully connected layers，FC）在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话，全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。在实际使用中，全连接层可由卷积操作实现：对前层是全连接的全连接层可以转化为卷积核为1×1的卷积；而前层是卷积层的全连接层可以转化为卷积核为hxw的全局卷积，h和w分别为前层卷积结果的高和宽

分组卷积

在普通的卷积操作中，一个卷积核对应输出特征图的一个通道，而每个卷积核又会作用在输入特征图的所有通道上，因此最终输出特征图的每个通道都与输入特征图的所有通道相连。也就是说，在普通的卷积操作，在“通道”这个维度上其实是“全连接”
的。
所谓分组卷积，其实就是讲输入通道和输出通道都划分为同样的组数，然后仅让处于相同组号的输入通道和输出通道相互进行“全连接”。即分组卷积 Group convolution ：将多个卷积核拆分为分组，每个分组单独执行一系列运算之后，最终在全连接层再拼接在一起。
通常每个分组会在单独的GPU 中训练，从而利用多GPU 来训练。
分组卷积的重点不在于卷积，而在于分组：在执行卷积之后，将输出的feature map 执行分组。然后在每个组的数据会在各个GPU 上单独训练。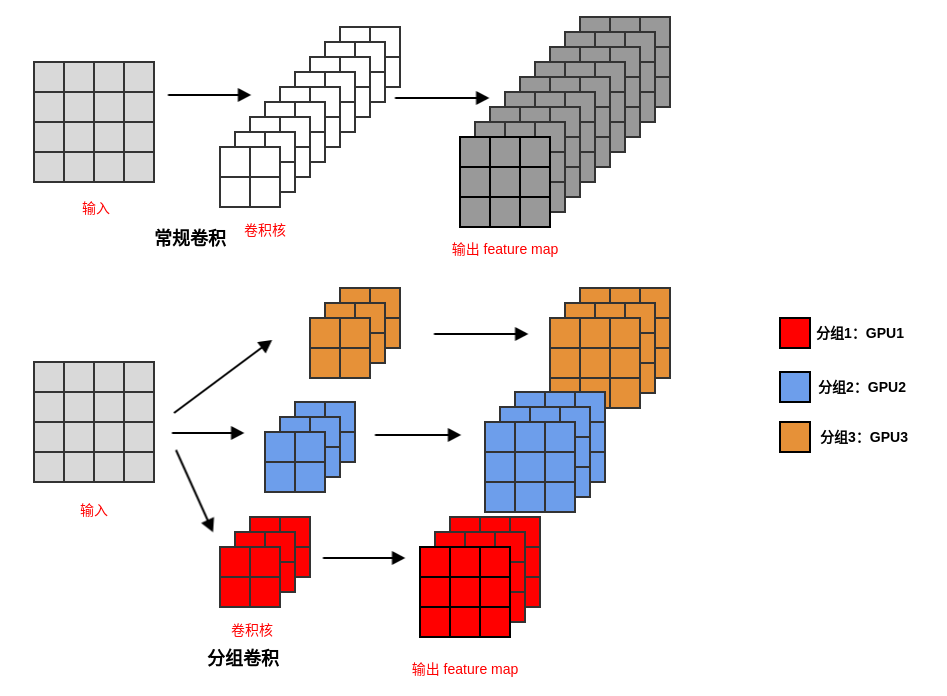

分组卷积在网络的全连接层才进行融合，这使得每个GPU 中只能看到部分通道的数据，这降低了模型的泛化能力。如果每次分组卷积之后，立即融合卷积的结果则可以解决这个问题。
分组卷积降低了模型的参数数量以及计算量。
假设输入feature map具有$C_I$的输入通道、宽/高分别为$W_I,H_I$，假设卷积核的宽/高分别为$W_K,H_K$，有$C_O$个卷积核。则：
参数数量为：$W_K\times H_K\times C_I\times C_O$
计算量为：$W_K\times H_K\times C_I\times W_O\times H_O\times C_O$。
假设采用分组卷积，将输入通道分成G组，则分组后：
参数数量为：$W_K\times H_K\times \frac{C_I}{G}\times \frac{C_O}{G}$
计算量为：$W_K\times H_K\times \frac{C_I}{G}\times W_O\times H_O\times \frac{C_O}{G}$
因此分组卷积的参数数量、计算量均为标准卷积计算的$\frac{1}{G}$。

小卷积核替代

在AlexNet 中用到了一些非常大的卷积核，如11x11、5x5 等尺寸的卷积核。卷积核的尺寸越大，则看到的图片信息越多，因此获得的特征会越好。但是卷积核的尺寸越大，模型的参数数量会爆涨，不利于模型的深度的增加，计算量和存储量也大幅上升。卷积核的尺寸越小，模型的参数数量越少，模型可以越深。但是卷积核的尺寸太小，则只能看到图片的一个非常小的局部区域，获得的特征越差。
解决方案是：用多个小卷积层的堆叠来代替较大的卷积核。
假设大卷积核的宽度是$k$，则每经过一层，输出的宽度减少了$k-1$。假设希望通过$n$个宽度为$k’$的小卷积核来代替，则为了保持输出的大小一致，需要满足：

$$k-1=n(k'-1)$$

如：用 2 个 3x3 的卷积核来代替1个 5x5 的卷积核。假设输入通道数为$C_I$，输出通道数为$C_O$，则5x5 卷积核的参数数量为$C_O\times C_I\times 5\times 5$；而 2个 3x3 卷积核的参数数量为$2\times C_O\times C_I\times 3\times 3$，是前者的 72% 。
用多个小卷积层的堆叠代替一个大卷积层的优点：
1）可以实现与大卷积层相同的感受野。
2）具有更大的非线性，网络表达能力更强。虽然卷积是线性的，但是卷积层之后往往跟随一个ReLU 激活函数。这使得多个小卷积层的堆叠注入了更大的非线性。
3）具有更少的参数数量。
小卷积层堆叠的缺点是：加深了网络的深度，容易引发梯度消失等问题，从而使得网络的训练难度加大。
通常选择使用3x3 卷积核的堆叠：
1）1x1 的卷积核：它无法提升感受野，因此多个1x1 卷基层的堆叠无法实现大卷积层的感受野。
2）2x2 的卷积核：如果希望输入的feature map 尺寸和输出的feature map 尺寸不变，则需要对输入执行非对称的padding。此时有四种padding 方式，填充方式的选择又成了一个问题。
3）3x3 的卷积核：可以提升感受野，对称性填充（不需要考虑填充方式），且尺寸足够小。

多尺度卷积核

图像中目标对象的大小可能差别很大。由于信息区域的巨大差异，为卷积操作选择合适的卷积核尺寸就非常困难。信息分布更具有全局性的图像中，更倾向于使用较大的卷积核。信息分布更具有局部性的图像中，更倾向于使用较小的卷积核。
一个解决方案是：分别使用多个不同尺寸的卷积核从而获得不同尺度的特征，然后将这些特征拼接起来。通过多种尺度的卷积核，无论感兴趣的信息区域尺寸多大，总有一种尺度的卷积核与之匹配。这样总可以提取到合适的特征。
多尺寸卷积核存在一个严重的问题：参数数量比单尺寸卷积核要多很多，这就使得计算量和存储量都大幅增长。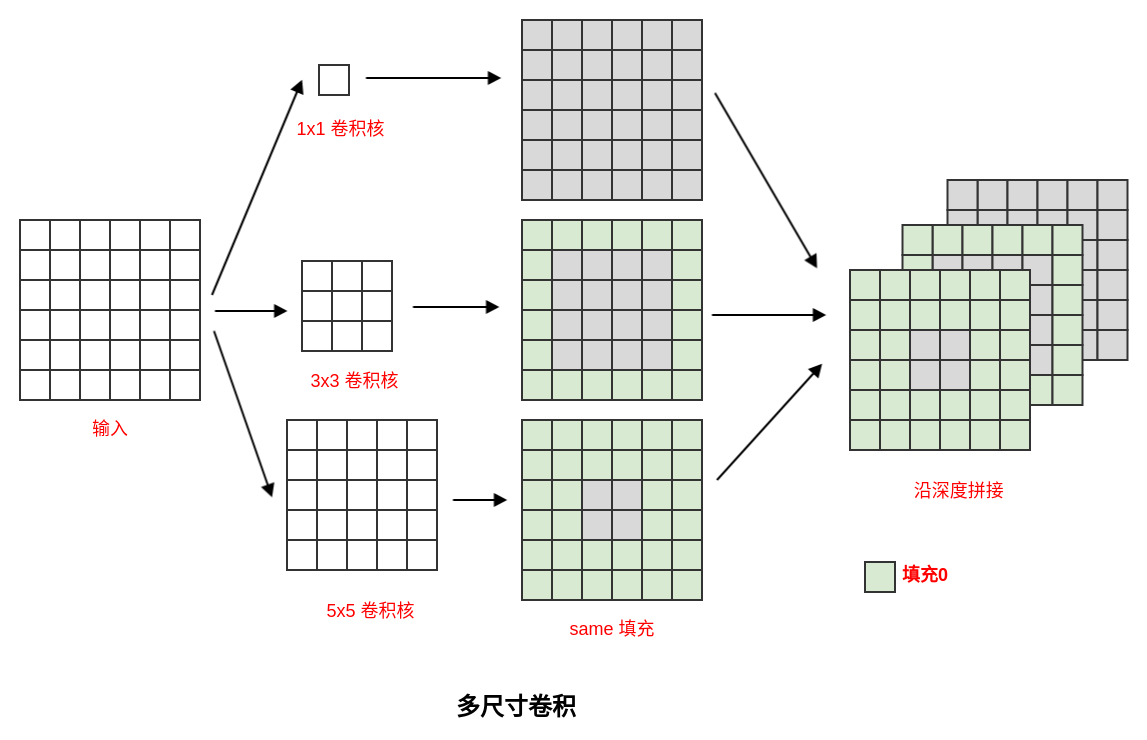

1x1卷积核

1x1 卷积并不是复制输入，它会进行跨通道的卷积。它有三个作用：
1）实现跨通道的信息整合。
2）进行通道数的升维和降维。
3）在不损失分辨率的前提下（即：feature map 尺寸不变），大幅增加非线性。事实上1x1 卷积本身是通道的线性组合，但是通常会在1x1卷积之后跟随一个ReLU 激活函数。
在前文中，输入feature map 先经过1x1 卷积的压缩，这会导致该段信息容量的下降；然后经过常规卷积，此段信息容量不变；最后经过1x1 卷积的膨胀，恢复了信息容量。整体而言模型的信息容量很像一个bottleneck，因此1x1 卷积层也被称作瓶颈层。

DepthWise卷积

标准的卷积会考虑所有的输入通道，而DepthWise 卷积会针对每一个输入通道进行卷积操作，然后接一个1x1 的跨通道卷积操作。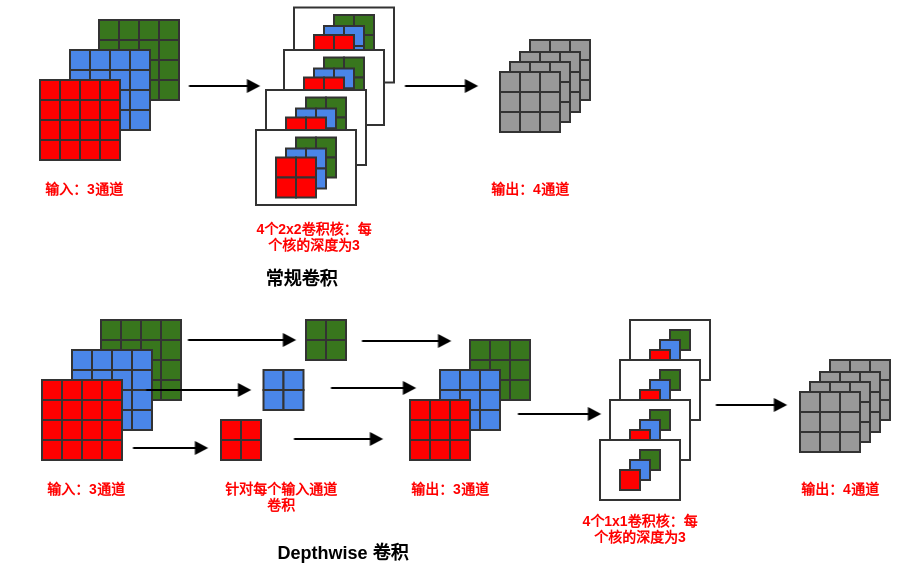

DepthWise 卷积与分组卷积的区别在于：
1）分组卷积是一种通道分组的方式，它改变的是对输入的feature map 处理的方式。Depthwise 卷积是一种卷积的方式，它改变的是卷积的形式。
2）Depthwise 分组卷积结合了两者：首先沿着通道进行分组，然后每个分组执行DepthWise 卷积。
假设使用标准卷积，输入通道的数量为$C_I$，输出通道的数量为$C_O$，卷积核的尺寸为$W_K\times W_K$。则需要的参数数量为$C_I\times W_K\times H_K\times C_O$。
使用Depthwise卷积时，图像的每个通道先通过一个$W_K\times H_K$的depthwise卷积层，再经过一个1x1、输出为$C_O$的卷积层。
参数量为：

$$C_I\times W_K\times H_K+C_I\times 1\times 1\times C_O=W_KH_KC_I+C_IC_O$$

其参数数量是标准卷积的$\frac{1}{C_O}+\frac{1}{W_KH_K}$。因此depthwise 卷积的参数数量远远小于标准卷积。

空洞卷积

在卷积神经网络中，一般会采用池化操作来扩大特征图的感受野，但这同时会降低特征图的分辨率，丢失一些信息（如内部数据结构、空间层级信息等），导致后续上采样操作（如转置卷积）无法还原一些细节，从而限制了最终分割精度的提升。
空洞卷积，顾名思义就是在标准的卷积中注入“空洞”，以增加卷积核的感受野。空洞卷积引入了扩张率（dilation rate）这个超参数来指定相邻采样点之间的间隔：扩展率为r的空洞卷积，卷积核上相邻数据点之间有r-1个空洞。扩张率为1的空洞卷积实际上就是普通卷积。空洞卷积利用空洞结构扩大了卷积核尺寸，不经过下采样操作即可增大感受野，同时还能保留输入数据的内部结构。

可变形卷积

普通的卷积操作是固定的、规则的网格点进行数据采样，这束缚了网络的感受野形状，限制了网络对几何形变的适应能力。为了克服这个限制，可变形卷积在卷积核的每个采样点上添加一个可学习的偏移量（offset），让采样点不再局限于规则的网格点。可变形卷积让网络具有了学习空间几何形变的能力。具体来说，可变形卷积引入了一个平行分支来端到端的学习卷积核采样点的位置偏移量，该平行分支先根据输入特征图计算出采样点的偏移量，然后在输入特征图上采样对应的点进行卷积运算。这种结构让可变形卷积的采样点能根据当前图像的内容进行自适应调整。

图像分类

给定一张图像，图像分类任务旨在判断该图像所属类别。

LeNet-5

LeCun等将BP算法应用到多层神经网络中，提出了LeNet5模型，并将其用于手写数字识别，卷积神经网络才算正式提出。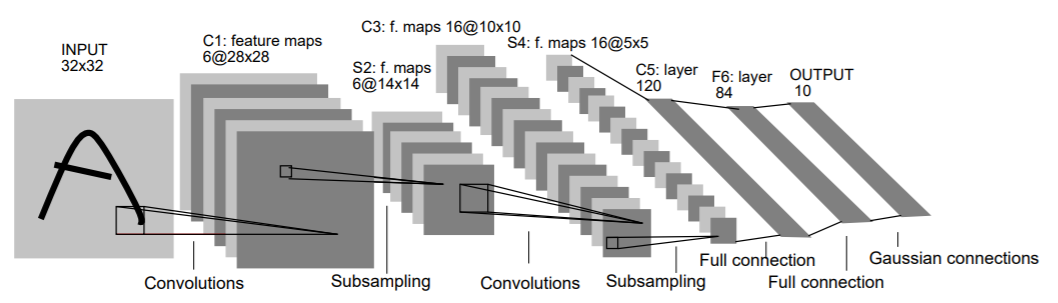


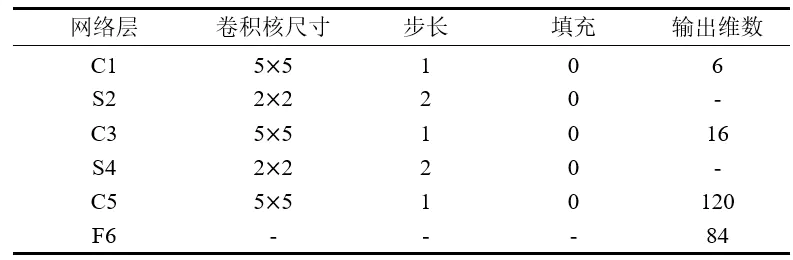
网络输入32*32的手写字体图片，这些手写字体包含0~9数字，也就是相当于10个类别的图片；输出：分类结果在0~9之间。LeNet的网络结构十分简单且单一，卷积层C1、C3和C5除了输出维数外采用的是相同的参数，池化层S2和S4采用的也是相同的参数。

AlexNet

2012年Krizhevsky使用卷积神经网络在ILSRC 2012图像分类大赛上夺冠，提出了AlexNet模型。AlexNet网络的提出对于卷积神经网络具有里程碑式的意义，相较于LeNet5的改进有以下几点：
1）数据增强：水平翻转、随机裁剪（平移变换）、颜色光照变换
2）Dropout:Dropout方法和数据增强一样，都是防止过拟合。dropout能按照一定的概率将神经元从网络中丢弃，dropout能在一定程度上防止过拟合，并且加快网络的训练速度。
3）ReLU激活函数：ReLU具有一些优良的特性，在为网络引入非线性的同时，也能引入稀疏性。稀疏性可以选择性激活和分布式激活神经元，能学习到相对稀疏的特征，起到自动化解离的效果。此外，ReLU的导数曲线在输入大于0时，函数的导数为1，这种特性能保证在其输入大于0时梯度不衰减，从而避免或抑制网络训练时梯度消失现象，网络模型的收敛速度会相对稳定。4）Local Response Normalization:局部响应归一化，简称LRN，实际就是利用临近的数据做归一化。5）Overlapping Pooling：即Pooling的步长比Pooling Kernel对应边要小。6）多GPU并行：极大加快网络训练。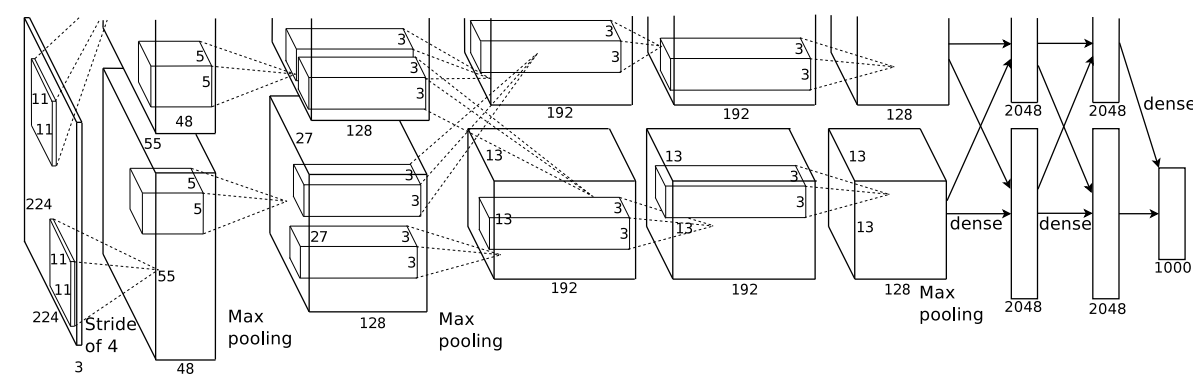

VGGNet

VGGNet是由牛津大学计算机视觉组合Google DeepMind项目的研究员共同研发的卷积神经网络模型，包含VGG16和VGG19两种模型。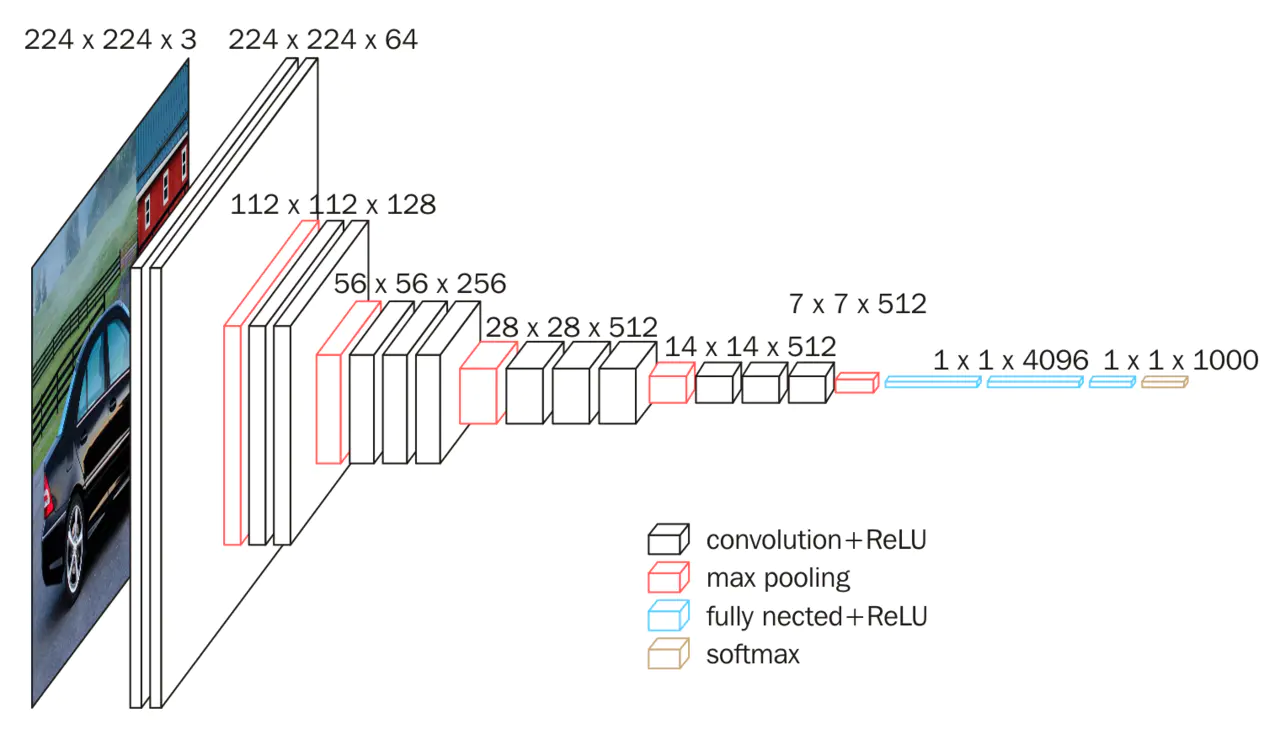

从网络模型中可以看出，VGG16相比于AlexNet类的模型具有较深的深度，通过反复堆叠$3\times 3$的卷积层和$2\times 2$的池化层，VGG16构建了较深层次的网络结构。与AlexNet主要有以下不同：
1）Vgg16有16层网络，AlexNet只有8层；
2）在训练和测试时使用了多尺度做数据增强。

GoogleNet(22层)

GoogleNet进一步增加了网络模型的深度，但是单纯的在VGG16的基础上增加网络的宽度会带来以下的缺陷：1）过多的参数容易引起过拟合；2）层数的过深，容易引起梯度消息现象。
GoogleNet的提出受到论文Network in Network(NIN)的启发，NIN有两个贡献：1）提出多层感知卷积层，使用卷积层后加上多层感知机，增强网络提取特征的能力。普通的卷积层和多层感知卷积层结构如图所示，Mlpconv相当于在一般卷积层后加一个1*1的卷积层。2）提出了全局平均池化代替全连接层，全连接层具有大量的参数，使用全局平均池化代替全连接层，能很大程度减少参数空间，便于加深网络，还能防止过拟合。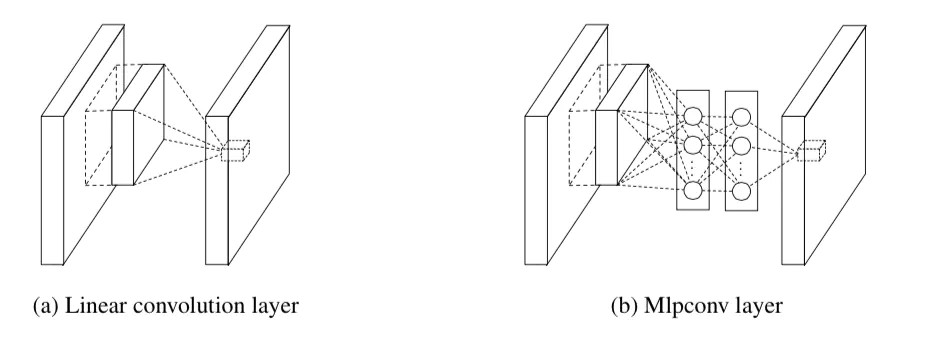

GoogleNet根据Mlpconv的思想提出了Inception结构，该结构有两个版本，下图是Inception的naive版，该结构巧妙的将$1\times 1$、$3\times 3$和$5\times 5$三种卷积核和最大池化层结合起来作为一层结构。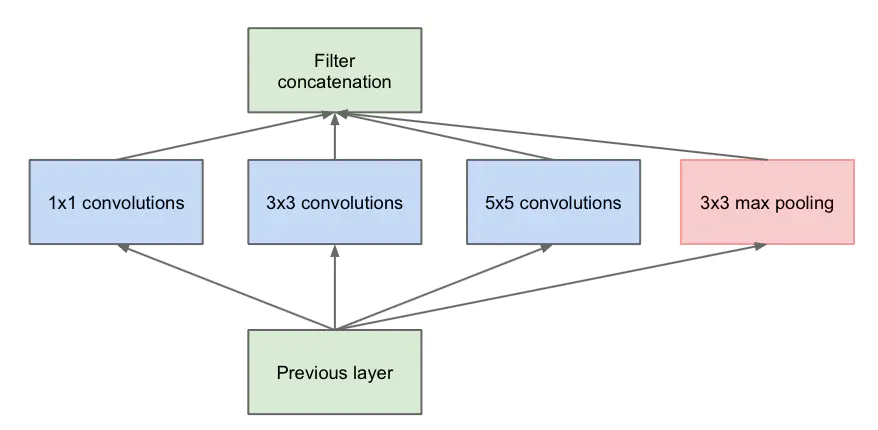

而Inception的native版中$5\times 5$的卷积核会带来很大的计算量，因此采用了与NIN类似的结构，在原始的卷积层之后加上$1\times 1$卷积层，最终版本的Inception如下图所示：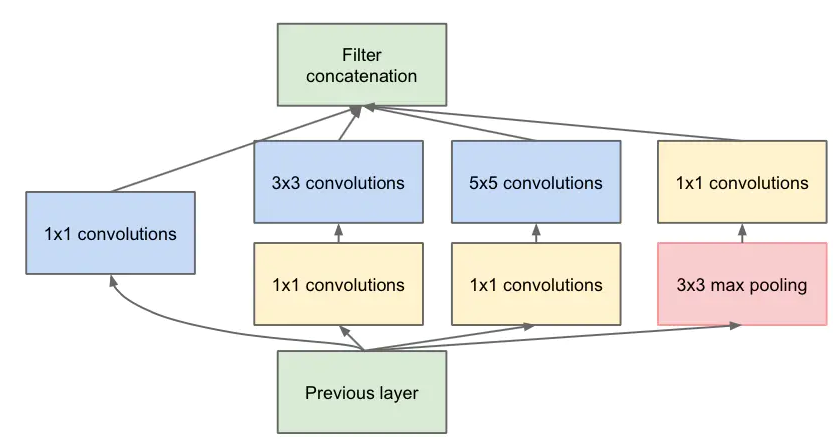

Inception v3/v4

在GoogleNet的基础上进一步降低参数，其和GoogleNet有相似的Inception模块，但将$7\times 7$和$5\times 5$卷积分解为若干等效$3\times 3$卷积，并在网络中后部分把$3\times 3$卷积分解为$1\times 3$和$3\times 1$卷积，这使得在相似的网络参数下网络可以部署到42层。此外，Inception v3使用了批量归一化层。Inception v3是GoogleNet计算量的2.5倍，而错误率较后者下降了3%。Inception v4在Inception模块基础上结合residual模块，进一步降低了0.4%的错误率。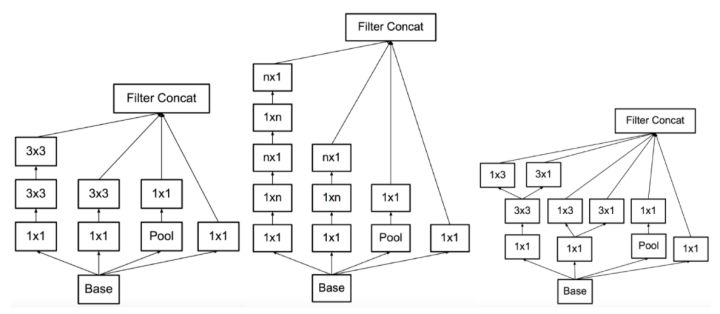

Inception v1/v2/v3/v4

Inception v1/v2/v3/v4对比

ResNet

卷积神经网络模型的发展历程一次次证明加深网络的深度和宽度能得到更好的效果，但是后来的研究发现，网络层次较深的网络模型的效果反而不如较浅层的网络，称为“退化”现象。退化现象产生的原因在于当模型的结构变得复杂随机梯度下降的优化变得更加困难，导致网络模型的效果反而不如浅层网络。针对这个问题，MSRA何凯明团队提出Residual Network，该网络具有Residual结构如下所示：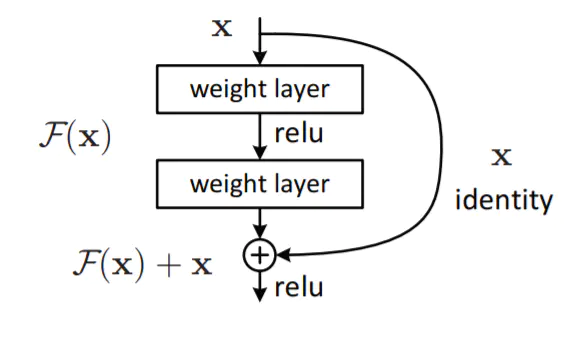

ResNet的基本思想是引入了能够跳过一层或多层的“shortcut connection”，即增加一个identity mapping（恒等映射），将原始所需要学的函数H(x)转换为F(x)+x，作者认为这两种表达的效果相同，但是优化的难度却并不相同。这个Residual block通过将shortcut connection实现，通过shortcut将这个block的输入和输出进行一个element-wise的叠加，这个简单地加法并不会给网络增加额外的参数和计算量，同时却可以大大增加模型的训练速度，提高训练效果，并且当模型的层数加深时，这个简单的结构能够很好的解决退化问题。
这种短连接的好处在于：
1）能缩短误差反向传播到各层的路径，有效抑制梯度消失现象，从而使网络在不断加深时性能不会下降。
2）由于有“近道”的存在，若网络在层数加深时性能退化，则它可以通过控制网络中“近道”和“非近道”的组合比例来退回到之前浅层的状态，即“近道”具备自我关闭能力。
对于shortcut的方式，作者提出了三个策略：1）使用恒等映射，如果residual block的输入和输出维度不一致，对增加的维度用0来填充；2）在block输入输出维度一致时使用恒等映射，不一致时使用线性投影以保证维度一致；3）对于所有的block使用线性投影。论文最后用三个$1\times 1,3\times 3, 1\times 1$的卷积层代替前面说的两个$3\times 3$卷积层，第一个$1\times 1$用来降低维度，第三个$1\times 1$用来增加维度，这样可以保证中间的$3\times 3$卷积层拥有比较小的输入输出维度。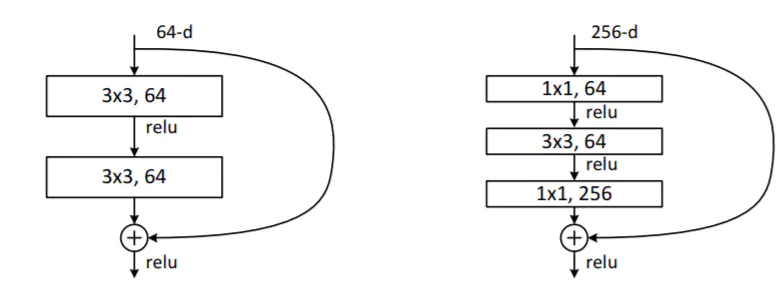

ResNet提出的背景和核心理论是什么？

提出背景：解决或缓解深层的神经网络训练中梯度消失的问题
ResNet的一个重要假设：假设有一个L层的深度神经网络, 如果我们在上面加入一层, 直观来讲得到的L+1层深度神经网络的效果应该至少不会比L层的差。因为可以简单的设最后一层为前一层的拷贝(相当于恒等映射), 并且其它层参数设置不变。
但是最终实验发现: 层数更深的神经网络反而会具有更大的训练误差, 因此, 作者认为深层网络效果差的原因很大程度上也许不在于过拟合, 而在于梯度消失问题。
解决办法：
根据梯度消失问题的根本原因所在(链式法则连乘), ResNet通过调整网络结构来解决上述问题。ResNet的结构设计思想为: 既然离输入近的神经网络层比较难训练, 那么我们可以将它短接到更靠近输出的层。输入x经过两个神经网络的变换得到F(x)， 同时也短接到两层之后， 最后这个包含两层的神经网络模块输出H(x)=F(x)+x。这样一来， F(x)被设计为只需要拟合输入x与目标输出H(x)的残差H(x)-x。在梯度更新期间，梯度的相关性会随着层数的变深呈指数性衰减，导致梯度趋近于白噪声，而skip-connections 可以减缓衰减速度，使相关性和之前比起来变大。

DenseNet

DenseNet网络介绍
DenseNet脱离了加深网络层数(ResNet)和旁路网络结构(Inception)来提升网络性能的定式思维，从特征的监督考虑，通过特征重用和旁路（Bypass）设置，既大幅度减少了网络的参数量，又在一定程度上缓解了梯度消失问题的产生。DenseNet作为另一种较深层数的卷积神经网络，具有如下优点：
1）相比于ResNet拥有更少的参数数量；2）旁路加强了特征的重用；3）网络更容易训练，并具有一定的正则效果；4）缓解了gradient vanishing和model degradation的问题。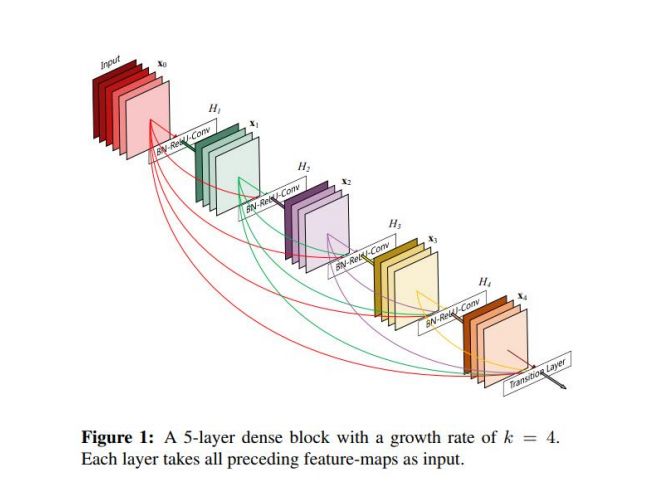

如图所示，第i层的输入不仅与i-1层的输出相关，还与所有之前层的输出相关。记作：
$Xl=H_l([X_0,X_1,…,X{l-1}])$
其中[]代表concatenation（拼接），既将$X0$到$X{l-1}$层的所有输出feature map按Channel组合在一起，这里所用到的非线性变换H为BN+ReLU+Conv(3x3)的组合。
由于在DenseNet中需要对不同层的feature map进行cat操作，所以需要不同层的feature map保持相同的feature size，这就限制了网络中的down sampling的实现。为了使用down sampling在实验中transition layer由BN+Conv(1x1)+average-pooling(2x2)组成。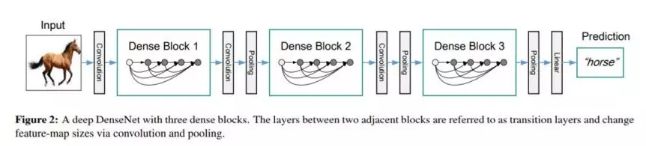

SENet

Squeeze-and-Excitation Networks（SENet）是由自动驾驶公司Momenta在2017年公布的一种全新的图像识别结构，它通过对特征通道间的相关性进行建模，把重要的特征进行强化来提升准确率。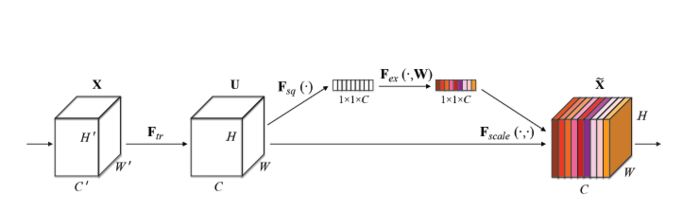

上图是SENet的Block单元，图中的$F{tr}$是传统的卷积结构，X和U是$F{tr}$的输入（C’xH’xW’）和输出（CxHxW），这些都是以往结构中已存在的。SENet增加的部分是U后的结构：对U先做一个Global Average Pooling（图中的$F{sq(.)}$，作者称为Squeeze过程），输出的1x1xC数据再经过两级全连接（图中的$F{ex(.)}$，作者称为Excitation过程），最后用sigmoid限制到[0，1]的范围，把这个值作为scale乘到U的C个通道上， 作为下一级的输入数据。这种结构的原理是想通过控制scale的大小，把重要的特征增强，不重要的特征减弱，从而让提取的特征指向性更强。
先是Squeeze部分。GAP有很多算法，作者用了最简单的求平均的方法，将空间上所有点的信息都平均成了一个值。这么做是因为最终的scale是对整个通道作用的，这就得基于通道的整体信息来计算scale。另外作者要利用的是通道间的相关性，而不是空间分布中的相关性，用GAP屏蔽掉空间上的分布信息能让scale的计算更加准确。

$$z_c=F_{sq}(u_c)=\frac{1}{W\times H}\sum_{i=1}^W\sum_{j=1}^Hu_c(i,j)$$

Excitation部分是用2个全连接来实现 ，第一个全连接把C个通道压缩成了C/r个通道来降低计算量（后面跟了RELU），第二个全连接再恢复回C个通道（后面跟了Sigmoid），r是指压缩的比例。作者尝试了r在各种取值下的性能 ，最后得出结论r=16时整体性能和计算量最平衡。
为什么要加全连接层呢？这是为了利用通道间的相关性来训练出真正的scale。一次mini-batch个样本的squeeze输出并不代表通道真实要调整的scale值，真实的scale要基于全部数据集来训练得出，而不是基于单个batch，所以后面要加个全连接层来进行训练。
可以拿SE Block和下面3种错误的结构比较来进一步理解：
下图最上方的结构，squeeze的输出直接scale到输入上，没有了全连接层，某个通道的调整值完全基于单个通道GAP的结果，事实上只有GAP的分支是完全没有反向计算、没有训练的过程的，就无法基于全部数据集来训练得出通道增强、减弱的规律。
下图中间是经典的卷积结构，有人会说卷积训练出的权值就含有了scale的成分在里面，也利用了通道间的相关性，为啥还要多个SE Block？那是因为这种卷积有空间的成分在里面，为了排除空间上的干扰就得先用GAP压缩成一个点后再作卷积，压缩后因为没有了Height、Width的成分，这种卷积就是全连接了。
下图最下面的结构，SE模块和传统的卷积间采用并联而不是串联的方式，这时SE利用的是$F_{tr}$输入X的相关性来计算scale，X和U的相关性是不同的，把根据X的相关性计算出的scale应用到U上明显不合适。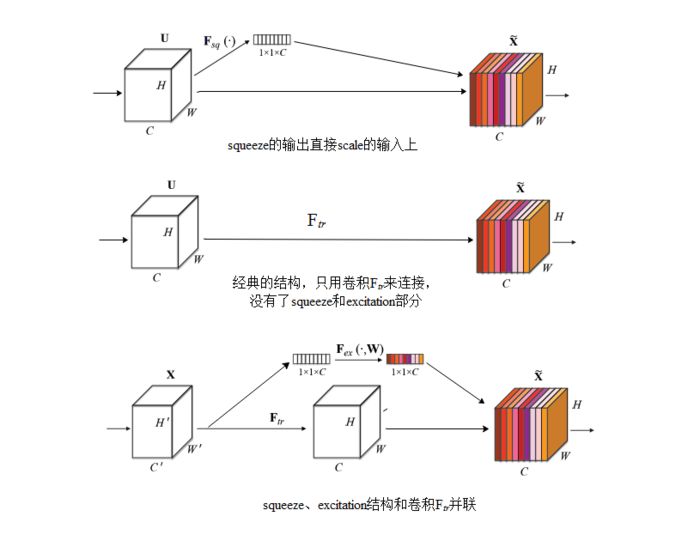

下图是两个SENet实际应用的例子，左侧是SE-Inception的结构，即Inception模块和SENet组和在一起；右侧是SE-ResNet，ResNet和SENet的组合，这种结构scale放到了直连相加之前。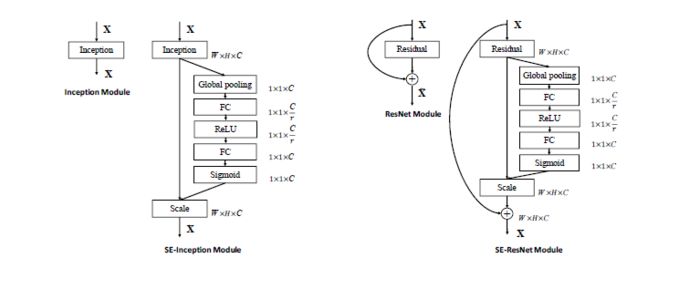

历年来所有的网络

LeNet-5:第一个卷积，用来识别手写数组，使用的卷积大小为5×5,s=1，就是普通的卷积核池化层结合起来，最后加上全连接层。
AlexNet:在第一个卷积中使用了11×11卷积，第一次使用Relu，使用了NormLayer，但不是我们经常说的BN。使用了dropout，并在两个GPU上进行了训练。
VGGNet:只使用了小卷积3×3(s=1)以及常规的池化层，不过深度比上一个深了一些，最后几层也都是全连接层接一个softmax。为什么使用3×3卷积，是因为三个3×3卷积的有效感受野和7×7的感受野一致，而且更深、更加非线性，卷积层的参数也更加地少，所以速度更快也可以适当加深层数。
GoogleNet:没有使用FC层，参数量相比之前的大大减少，提出了Inception module结构，也就是NIN结构(network within a network)。但是原始的Inception module计算量非常大，所以在每一个分支加了1×1 conv “bottleneck”结构。googlenet网络结构中为了避免梯度消失，在中间的两个位置加了两个softmax损失，所以会有三个loss，整个网络的loss是通过三个loss乘上权重相加后得到。
inception结构的特点：
1）增加了网络的宽度，同时也提高了对于不同尺度的适应程度。
2）使用 1×1 卷积核对输入的特征图进行降维处理，这样就会极大地减少参数量，从而减少计算量。
3）在V3中使用了多个小卷积核代替大卷积核的方法，除了规整的的正方形，我们还有分解版本的 3×3 = 3×1 + 1×3，这个效果在深度较深的情况下比规整的卷积核更好。
4）发明了Bottleneck 的核心思想还是利用多个小卷积核替代一个大卷积核，利用 1×1 卷积核替代大的卷积核的一部分工作。也就是先1×1降低通道然后普通3×3然后再1×1回去。
ResNet：其基本思想是引入了能够跳过一层或多层的“shortcut connection”，即增加一个identity mapping（恒等映射），将原始所需要学的函数H(x)转换为F(x)+x，作者认为这两种表达的效果相同，但是优化的难度却并不相同。这个Residual block通过将shortcut connection实现，通过shortcut将这个block的输入和输出进行一个element-wise的叠加，这个简单地加法并不会给网络增加额外的参数和计算量，同时却可以大大增加模型的训练速度，提高训练效果，并且当模型的层数加深时，这个简单的结构能够很好的解决退化问题。
DenseNet:ResNet是更一般的模型，DenseNet是更特化的模型。DenseNet用于图像处理可能比ResNet表现更好，本质是DenseNet更能和图像的信息分布特点匹配，是使用了多尺度的Kernel。densenet因为需要重复利用比较靠前的feature map，导致显存占用过大，但正是这种通道特征的concat造成densenet能更密集的连接。
SeNet：全称为Squeeze-and-Excitation Networks。核心思想就是去学习每个特征通道的重要程度，然后根据这个重要程度去提升有用的特征并抑制对当前任务用处不大的特征。这个给每一个特征层通道去乘以通过sigmoid得到的重要系数，其实和用bn层去观察哪个系数重要一样。

图像检测

分类任务关系整体，给出的是整张图片的内容描述，而检测则关注特定的物体目标，要求同时获得这一目标的类别信息和位置信息。相比于分类，检测给出的是对图片前景和背景的理解，我们需要从背景中分离出感兴趣的目标，并确定这一目标的描述（类别和位置）。因此，检测模型的输出是一个列表，列表的每一项使用一个数据组给出检测目标的类别和位置（常用矩形检测框的坐标表示）。
目前主流的目标检测算法主要是基于深度模型，大致可以分成两大类别：（1）One-Stage目标检测算法，这类检测算法不需要Region Proposal阶段，可以通过一个Stage直接产生物体的类别概率和位置坐标值，比较典型的算法有YOLO、SSD和CornerNet；（2）Two-Stage目标检测算法，这类检测算法将检测问题划分为两个阶段，第一个阶段首先产生候选区域（Region Proposals），包含目标大概的位置信息，然后第二个阶段对候选区域进行分类和位置精修，这类算法的典型代表有R-CNN、Fast R-CNN、Faster R-CNN等。目标检测模型的主要性能是检测准确度和速度，其中准确度主要考虑物体的定位及分类准确度。一般情况下，Two-Stage算法在准确度上有优势，而One-Stage算法在速度上有优势。不过随着研究的发展，两类算法都在两个方面做改进，均能在准确度及速度上取得较好结果。

IOU的定义

手写IOU
物体检测需要定位出物体的bounding box，对于bounding box的定位精度，存在一个定位精度评价公式：IOU。
IOU定义了两个bounding box的重叠度，如下图所示：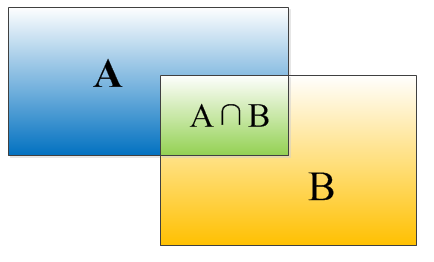

矩形框A、B的一个重合度计算公式为：

$$IOU=\frac{A\cap B}{A\cup B}$$

就是矩形框A、B的重叠面积$S_I$占A、B并集的面积的比例：

$$IOU=\frac{S_I}{S_A+S_B-S_I}$$

非极大值抑制

在目标检测时一般会采取窗口滑动的方式，在图像上生成很多的候选框，把这些候选框进行特征提取送入到分类器，一般会得到一个得分，然后把这些得分全部排序。选取得分最高的那个框，接下来计算其他框与当前框的重合程度(IOU)，如果重合程度大于一定的阈值就删除，这样不停的迭代下去就会得到所有想要找到的目标物体的区域。

Soft-NMS

非极大值抑制算法改进

R-CNN

算法摘要：首先输入一张图片，我们先定位出2000个物体候选框，然后采用CNN提取每个候选框中图片的特征向量，特征向量的维度是4096维，接着采用SVM算法对各个候选框中的物体进行分类识别。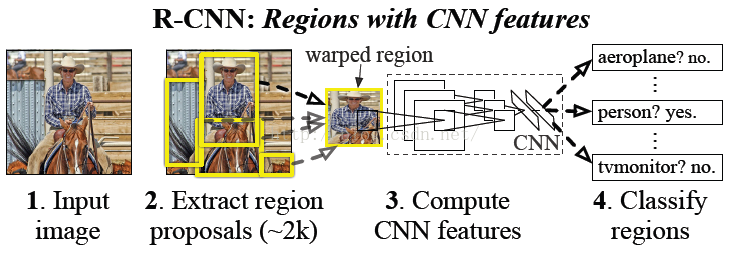

我们采用selective search算法搜索出候选框，由于搜索到的候选框是矩形的，而且大小各不相同，而CNN对输入的图片大小是固定的，因此需要对每个输入的候选框都要缩放到固定的大小。然而人工标注的图片中就只标注了一个正确的bounding box，我们搜索出来的2000个矩形框也不可能会出现一个与人工标注完全匹配的候选框。因此我们需要用IOU为2000个bounding box打标签，以便下一步CNN训练使用。在CNN阶段，如果用selective search挑选出来的候选框与物体的人工标注矩形框的重叠区域大于0.5，我们就把这个候选框标注成物体类别，否则我们就把它当做背景类别。最后，我们需要对上面预训练的CNN模型进行fine-tuning训练。假设需要检测的物体类别有N类，那么我们就需要将上面与训练的CNN模型的最后一层给替换点，替换成N+1个输出的神经元（还有一个背景），然后这一层直接采用参数随机初始化的方法，其他的网络层数不变。
R-CNN缺点：
1）耗时的selective search，对一帧图像，需要花费2s。
2）耗时的串行式CNN前向传播，对于每一个ROI，都需要经过一个AlexNet提取特征，为所有的ROI提供特征需要花费47s。
3）三个模块分别训练，并且在训练的时候，对于存储空间的消耗很大。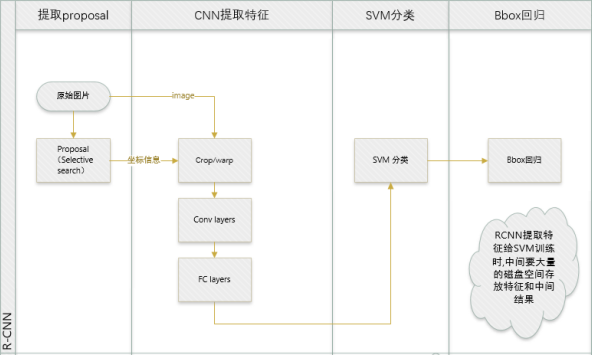

SPP-Net

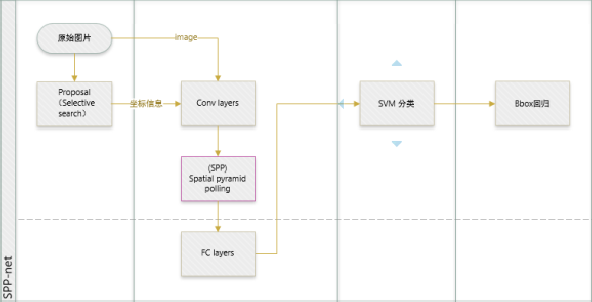
算法特点：1）通过Spatial Pyramid Pooling解决了深度网络固定输入层尺寸的这个限制，使得网络可以享受不限制输入尺寸带来的好处。2）解决了RCNN速度慢的问题，不需要对每个Proposal(2000个左右)进行wrap或crop输入CNN提取feature map，只需要对整图提一次feature map，然后将proposal区域映射到卷积特征层得到全连接层的输入特征。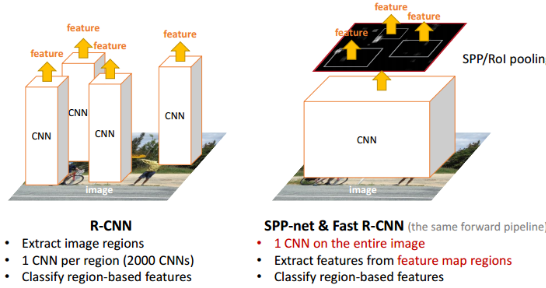

一、ROI在特征图上的对应的特征区域的维度不满足全连接层的输入要求怎么办？
事实上，CNN的卷积层不需要固定尺寸的图像，而是全连接层是需要固定大小的输入。根据Pooling规则，每个Pooling bin对应一个输出，所以最终的Pooling后的输出特征由bin的个数来决定。SPP网络就是分级固定bin的个数，调整bin的尺寸来实现多级Pooling固定输出。如图所示，SPP网络中最后一个卷积层的feature map维数为16x24，按照图中所示分为3级：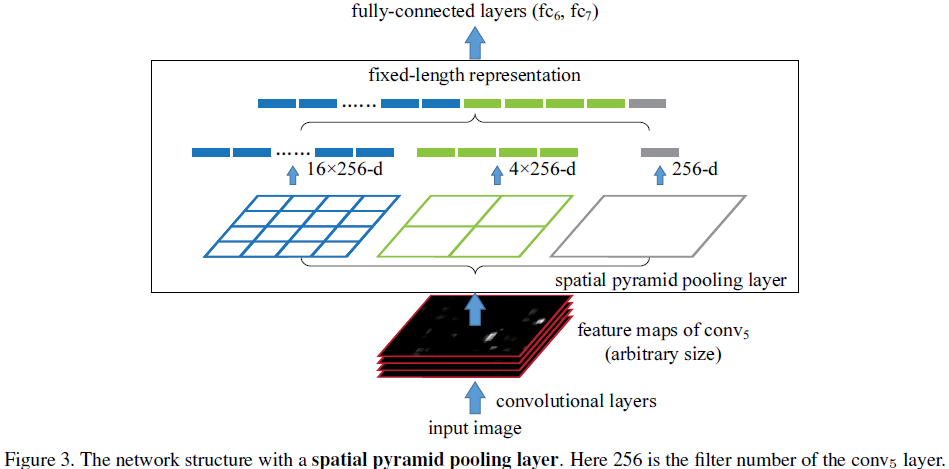

其中，第一级bin个数为1，最终对应的window大小为16x24；第二级bin个数为4个，最终对应的window大小为4x8；第三级bin个数为16个，最终对应的window大小为1x1.5(小数需要舍入处理)。通过融合各级bin的输出，最终每一个feature map经过SPP处理后，得到1+4+16维的feature map，经过融合后输入分类器。这样就可以在任意输入size和scale下获得固定的输出；不同的scale下网络可以提取不同尺度的特征，有利于分类。
二、原始图像的ROI如何映射到特征图？
下面将从感受野、感受野上坐标映射及原始图像的ROI如何映射三方面阐述。
1）感受野
在卷积神经网络中，感受野的定义是卷积神经网络每一层输出的特征图(feature map)的像素点在原始图像上映射的区域大小。

$$output\ field\ size = (input\ field\ size - kernel size + 2*padding) / stride + 1$$

其中output field size是卷积层的输出，input field size是卷积层的输入，反过来卷积层的输入为:

$$input\ field\ size = (output\ field\ size - 1) * stride - 2*padding + kernel size$$

2）感受野上的坐标映射
对于Convolution/Pooling Layer:

$$p_i=s_i \cdot p_{i+1}+[(k_i-1)/2-padding]$$

对于Neuronlayer（ReLU/Sigmoid/…）:

$$p_i=p_{i+1}$$

其中$pi$为第$i$层感受野上的坐标，$s_i$为Stride的大小，$k_i$为感受野的大小。
何凯明在SPP-NET中使用的是简化版本，将公式中的Padding都设为$\left \lfloor k_i/2 \right \rfloor$，公式可进一步简化为：$$p_i=s_i \cdot p{i+1}$$
3）原始图像的ROI如何映射
SPP-NET是把原始ROI的左上角和右下角 映射到Feature Map上的两个对应点。 有了Feature Map上的两队角点就确定了对应的Feature Map 区域（下图中橙色）。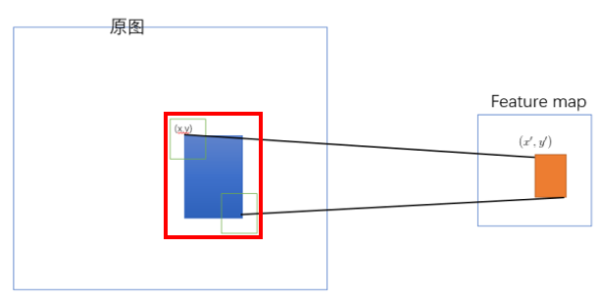

左上角取$x’=\left \lfloor x/S \right \rfloor+1, y’=\left \lfloor y/S \right \rfloor+1$；右下角的点取$x’=\left \lceil x/S \right \rceil-1, y’=\left \lceil y/S \right \rceil-1$。其中S为坐标映射的简化计算版本，即$S=\prod_{0}^{i}s_i$。
ROI pooling具体操作：
1）根据输入image，将ROI映射到feature map对应位置。
2）将映射后的区域划分为相同大小的sections（sections数量和输出的维度相同）；
3）对每个sections进行max pooling操作。
这样就可以从不同大小的方框得到固定大小的相应的feature maps。
ROI原理

Fast R-CNN

Fast R-CNN针对R-CNN在训练时multi-state pipeline和训练的过程很耗时间和空间的问题进行了改进，主要改进为：
1）在最后一个卷积层加了一个ROI pooling layer。ROI Pooling layer首先可以将image中的ROI定位到feature map，然后用一个单层的SPP layer将这个feature map池化到固定大小的feature map后再传入全连接层。
2）损失函数使用多任务损失函数（multi-task loss），将边框回归直接加入到CNN网络进行训练。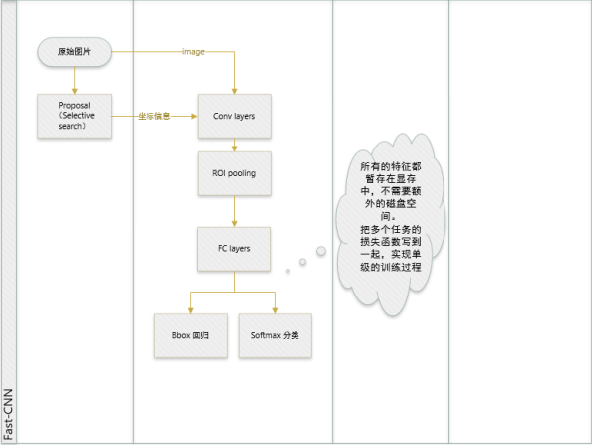

首先还是采用selective search提取2000个候选框，然后对全图进行特征提取，接着使用一个ROI pooling layer在全体特征上获取每一个ROI对应的特征，再通过全连接层进行分类和检测框修正。即最后得到的ROI feature vector被分开，一个经过全连接层后用作softmax回归，用来分类，另一个经过全连接后用作bbox回归。需要注意的是，输入到后面ROI Pooling layer的feature map是在卷积层上的feature map上提取的，故整个特征提取过程只计算一次卷积。虽然在最开始也提取了大量的ROI，但他们还是作为整体输入到卷积网络的，最开始提取的ROI区域只是为了最后的bounding box回归时使用。
联合训练：联合训练（Joint Training）指如何将分类和边框回归联合到一起在CNN阶段训练，主要难点是损失函数的设计。Fast-RCNN中，有两个输出层：第一个是针对每个ROI区域的分类概率预测，$p=(p_0, p_1, \cdots, p_K)$；第二个则是针对每个ROI区域坐标的偏移优化，$t^k = (t^k_x, t^k_y, t^k_w, t^k_h)$，$0 \le k \le K$是多类检测的类别序号。每个训练ROI都对应着真实类别$u$和边框回归目标$v=(v_x,v_y,v_w,v_h)$，对于类别$u$预测边框为$t^u=(t_x^u,t_y^u,t_w^u,t_h^u)$，使用多任务损失$L$来定义ROI上分类和边框回归的损失：

$$L(p,u,t^u,v)=L_{cls}(p,u)+\lambda [u \ge 1]L_{loc}(t^u,v)$$

其中$L_{cls}(p,u)=-\log p_u$表示真实类别的log损失，当$u \ge 1$时，$[u \ge 1]$的值为1，否则为0。下面将重点介绍多任务损失中的边框回归部分（对应坐标偏移优化部分）。
边框回归：假设对于类别$u$，在图片中标注的真实坐标和对应的预测值理论上两者越接近越好，相应的损失函数为：

$$L_{loc}(t^u, v) = \sum_{i \in {x, y, w, h}} \text{smooth}_{L_1}(t_i^u- v_i)$$ $$\text{smooth}_{L_1}(x) = \left \{ \begin{aligned} & 0.5x^2 & |x| \le 1 \\ &|x|-0.5 & \text{otherwise}\end{aligned} \right.$$

Fast-RCNN在上面用到的鲁棒$L1$函数对外点比RCNN和SPP-NET中用的$L_2$函数更为鲁棒，该函数在$(-1, 1)$之间为二次函数，其他区域为线性函数。
存在问题：使用Selective Search提取Region Proposals，没有实现真正意义上的端到端，操作耗时。
采用$\text{smooth}{L_1}$的原因：边框的预测是一个回归问题，通常可以选择平方损失函数（L2损失）$f(x)=x^2$，但这个损失对于比较大的误差的惩罚很高。可以采用稍微缓和一点绝对损失函数（L1损失）$f(x)=|x|$，这个函数在0点处导数不存在，因此可能会影响收敛。因此采用分段函数，在0点附近使用平方函数使得它更加平滑。

Faster R-CNN

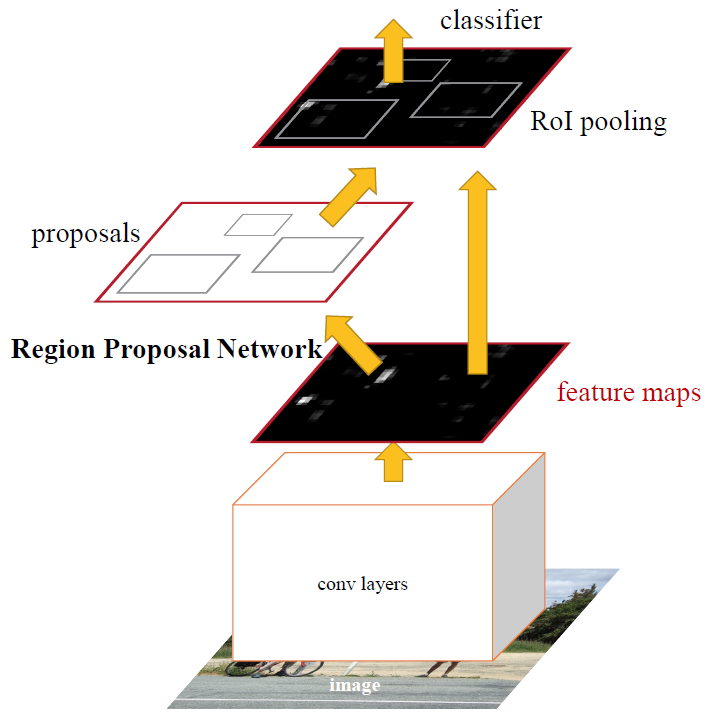
算法特点：1）提出了Region Proposal Network(RPN)，将Proposal阶段和CNN分类融合到一起，实现了一个完全的End-To-End的CNN目标检测模型。RPN可以快速提取高质量的Proposal，不仅加快了目标检测速度，还提高了目标检测性能。2）将Fast R-CNN和RPN放在同一个网络结构中训练，共享网络参数。

Region Proposal Network

Region Proposal Network(RPN)的核心思想是使用卷积神经网络直接产生Region Proposal，使用的方法本质上就是滑动窗口。RPN的设计比较巧妙，RPN只需要在最后的卷积层上滑动以便，借助Anchor机制和边框回归就可以得到多尺度多长宽比的Region Proposal。下图是RPN的网络结构图。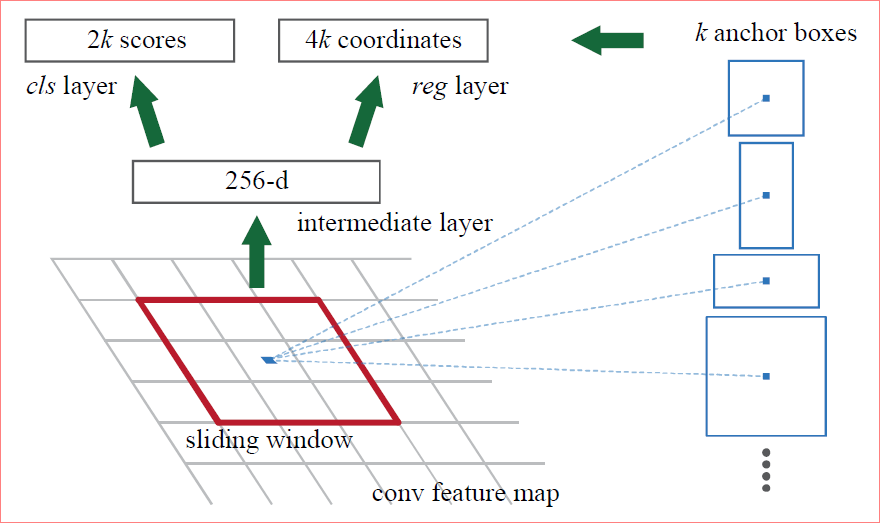

给定输入图像（假设分辨率为$600*1000$），经过卷积操作得到最后一层卷积特征图（大小约为$40\times 60$）。在这个特征图上使用$3\times 3$的卷积核（滑动窗口）与特征图进行卷积，最后一层卷积层共有256个feature map，那么这个$3\times 3$的区域卷积后可以获得一个256维的特征向量，后边接cls layer和reg layer分别用于分类和边框回归（跟Fast R-CNN类似，只不过这里的类别只有目标和背景两个类别）。$3\times 3$滑窗对应的每个特征区域同时预测输入图像的3种尺度（128，256，512），3中长宽比（1：1，1：2，2：1）的Region Proposal，这种映射的机制称为Anchor。所以对于这个$40\times 60$的feature map，总共有约20000（$40\times 60\times 9$）个Anchor，也就是预测20000个Region Proposal。一般来说原始输入图片都要缩放到固定的尺寸才能作为网络的输入，这个尺寸在作者源码里限制成800x600，9种anchor还原到原始图片上基本能覆盖800x600图片上各种尺寸的坐标。
Anchor是在原图上的区域而不是在特征图上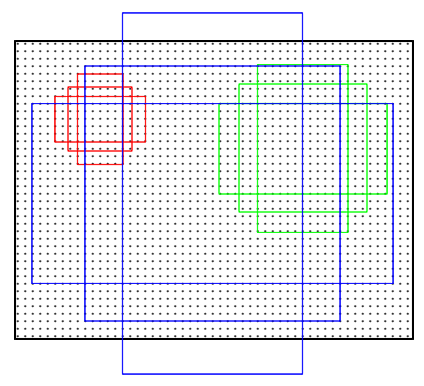

这样设计的好处是什么？虽然现在也是在用的滑动窗口策略，但是滑动串口操作是在卷积特征图上进行的，维度较原始图像降低了$16\times 16$倍；多尺度使用了9中Anchor，对应了三种尺度和三种长宽比，加上后边接了边框回归，所以几遍是这9种Anchor外的窗口也能得到一个跟目标比较接近的Region Proposal。
anchor讲解

RPN的损失函数

损失函数的定义为：

$$L({p_i}{t_i}) = \frac{1}{N_{cls}} \sum_i L_{cls}(p_i, p_i^*) +\lambda \frac{1}{N_{reg}} \sum_i p_i^* L_{reg}(t_i, t_i^*)$$

其中$i$表示一次Mini-Batch中Anchor的索引，$pi$是Anchor $i$是否是一个物体，$L{reg}$即为上面提到的$\text{smooth}{L_1}(x)$函数，$N{cls}$和$N_{reg}$是两个归一化项，分别表示Mini-Batch的大小和Anchor位置的数目。

网络的训练

作者采用了4-step Alternating Training:
1) 用ImageNet模型初始化，独立训练一个RPN网络；
2) 仍然用ImageNet模型初始化，但是使用上一步RPN网络产生的Proposal作为输入，训练一个Fast-RCNN网络，至此，两个网络每一层的参数完全不共享；
3) 使用第二步的Fast-RCNN网络参数初始化一个新的RPN网络，但是把RPN、Fast-RCNN共享的那些卷积层的Learning Rate设置为0，也就是不更新，仅仅更新RPN特有的那些网络层，重新训练，此时，两个网络已经共享了所有公共的卷积层；
4) 仍然固定共享的那些网络层，把Fast-RCNN特有的网络层也加入进来，形成一个Unified Network，继续训练，Fine Tune Fast-RCNN特有的网络层，此时，该网络已经实现我们设想的目标，即网络内部预测Proposal并实现检测的功能。
在训练分类器和RoI边框修正时，步骤如下：
1）首先通过RPN生成约20000个anchor（40x60x9）
2）对20000个anchor进行第一次边框修正，得到修订边框后的proposal；
3）对超过图像边界的proposal的边进行clip，使得该proposal不超过图像范围；
4）忽略掉长或宽太小的proposal；
5）将所有的proposal按照前景分数从高到低排序，选取前12000个proposal；
6）使用阈值为0.7的NMS算法排除掉重叠的proposal；
7）针对上一步剩下的proposal，选取前2000个proposal进行分类和第二次边框修正。

Mask R-CNN

ROI Align是在Mask R-CNN这篇论文里提出的一种区域特征聚集方式，很好地解决了ROI Pooling操作中两次量化造成的区域不匹配的问题。在检测阶段将ROI Pooling替换为ROI Align可以提升检测模型的准确性。
在常见的两级检测框架中，ROI Pooling的作用是根据候选框的位置坐标在特征图中将相应的区域池化为固定尺寸的特征图，以便后续的分类和bounding box回归操作。由于预选框的位置通常是由模型回归得到的，一般来讲都是浮点数，而池化后的特征图要求尺寸固定，故ROI Pooling这一操作存在两次量化的过程。1）将候选框的边界量化为整数点坐标值。2）将量化后的边界区域平均分割成$k\times k$个单元（bin），对每一个单元的边界进行量化。经过上述的两次量化，此时的候选框已经和最开始回归出来的位置存在一定的偏差，这个偏差会影响检测或分割的精确度。在论文里作者将它归结为“不匹配问题(misalignment)”。
下面我们用直观的例子具体分析一下上述区域不匹配问题。如图所示，这是一个Faster-RCNN检测框架。输入一张$800\times 800$的图片，图片上有一个$665\times 665$的包围框(框着一只狗)。图片经过主干网络提取特征后，特征图缩放步长（stride）为32。因此，图像和包围框的边长都是输入时的1/32。800正好可以被32整除变为25。但665除以32以后得到20.78，带有小数，于是ROI Pooling 直接将它量化成20。接下来需要把框内的特征池化$7\times 7$的大小，因此将上述包围框平均分割成$7\times 7$个矩形区域。显然，每个矩形区域的边长为2.86，又含有小数。于是ROI Pooling 再次把它量化到2。经过这两次量化，候选区域已经出现了较明显的偏差（如图中绿色部分所示）。更重要的是，该层特征图上0.1个像素的偏差，缩放到原图就是3.2个像素。那么0.8的偏差，在原图上就是接近30个像素点的差别，这一差别不容小觑。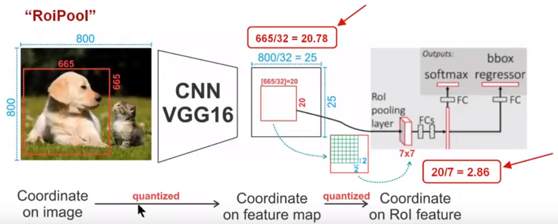

为了解决ROI Pooling的上述缺点，作者提出了ROI Align这一改进的方法。ROI Align的思路很简单：取消量化操作，使用双线性内插的方法获得坐标为浮点数的像素点上的图像数值，从而将整个特征聚集过程转化为一个连续的操作。ROI Align流程如下：
1）遍历每一个候选区域，保持浮点数边界不做量化；2）将候选区域分割成$k\times k$个单元，每个单元的边界也不做量化；3）在每个单元中计算出固定的四个坐标位置，用双线性内插的方法计算出这四个位置的值，然后进行最大池化的操作。
需要注意的是，这个固定位置是指在每一个矩形单元（bin）中按照固定规则确定的位置。比如，如果采样点数是1，那么就是这个单元的中心点。如果采样点数是4，那么就是把这个单元平均分割成四个小方块以后它们分别的中心点。显然这些采样点的坐标通常是浮点数，所以需要使用插值的方法得到它的像素值。事实上，ROI Align 在遍历取样点的数量上没有ROIPooling那么多，但却可以获得更好的性能，这主要归功于解决了misalignment的问题。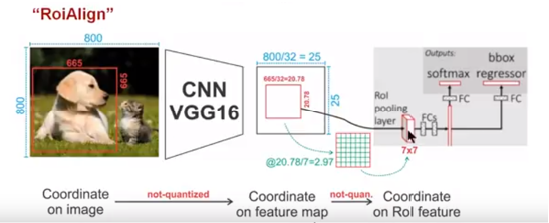


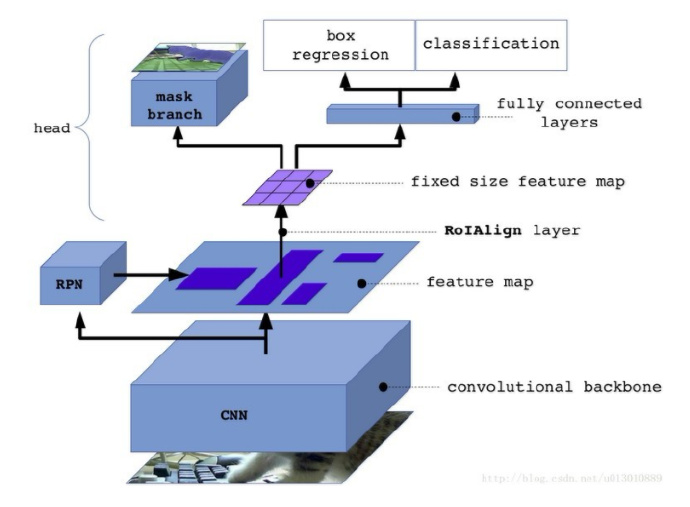
注意的是，在Mask R-CNN中的ROI Align之后有一个“head”部分，主要作用是将ROI Align的输出维度扩大，这样在预测Mask时会更加精确。
在Mask Branch的训练环节，作者没有采用FCN式的SoftmaxLoss，反而是输出了K个Mask预测图（为每一个类都输出一张），并采用average binary cross-entropy loss训练，当然在训练Mask branch的时候，输出K个特征图中，也就是对应ground truth类别的哪一个特征图对Mask loss有贡献。也就是说， Mask RCNN定义为多任务损失为$L=L{class}+L{boxes}+L{mask}$。
$L{class}$与$L{boxes}$与Faster RCNN没区别。$L{mask}$中，假设一共有K个类别，则mask分割分支的输出维度是$K\times m\times m$，对于$m\times m$中的每个点，都会输出K个二值Mask(每个类别使用sigmoid输出)。需要注意的是，计算loss的时候，并不是每个类别的sigmoid输出都计算二值交叉熵损失，而是该像素属于哪个类，哪个类的sigmoid输出才要计算损失函数，并且在测试的时候，我们通过分类分支预测类别来选择相应的mask预测。这样，mask预测和分类分支预测就彻底解耦了。

FPN

特征金字塔网络FPN
在物体检测里面，在有限的计算量的情况下，网络的深度（对应到感受野）与 stride 通常是一对矛盾的东西，常用的网络结构对应的 stride 一般会比较大（如 32），而图像中的小物体甚至会小于 stride 的大小，造成的结果就是小物体的检测性能急剧下降。传统解决这个问题的思路包括：
（1）多尺度训练和测试，有称图像金字塔，如图（a）所示。目前几乎所有在 ImageNet 和 COCO 检测任务上取得好成绩的方法都使用了图像金字塔方法。然而这样的方法由于很高的时间及计算量消耗，难以在实际中应用。
（2）特征分层，即每层分别预测对应的scale分辨率的检测结果，如图（c）所示。SSD检测框架采用了相似的思想，这样的方法的问题在于直接强行让不同层学习同样的语义信息，而对于卷积神经网络而言，不同的深度对应着不同层次的语义特征，浅层网络的分辨率高，学的更多是细节特征，深层网络分辨率低，学的更多是语义特征。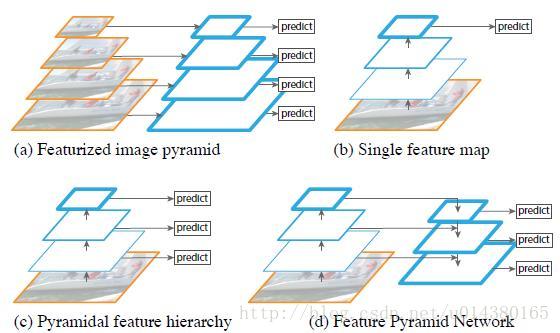

目前多尺度的物体检测主要面临的挑战是：
1）如何学习具有强语义信息的多尺度特征表示？
2）如何设计通用的特征表示来解决物体检测中的多个子问题？如object proposal,box localization,instance segmentation.
3）如何高效计算多尺度的特征表示？
本文针对这些问题，提出了特征金字塔FPN，如图（d）所示，网络直接在原来的按网络上做修改，每个分辨率的feature map引入后，将分辨率缩放两倍的feature map做element-wise相加的操作。通过这样的连接，每一层预测所用的feature map都融合了不同分辨率、不同语义强度的特征，融合的不同分辨率的feature map分别做对应分辨率的物体检测。这样保证了每一层都有合适的分辨率以及强语义特征。同事，由于此方法只是在原网络的基础上家里额外的跨层连接，在实际应用中几乎不增加额外的时间和计算量。
自下而上的路径
CNN的前馈计算就是自下而上的路径，特征图经过卷积核计算，通常是越变越小，也有一些特征层的输出和原来的大小一样，称为“相同网络阶段”。对于本文的特征金字塔，作者为每个阶段定义一个金字塔级别，然后选择每个阶段的最后一层的输出作为特征图的参考集，这是因为每个阶段的最深层应该具有最强的特征。具体来说，对于ResNets，作者使用了每个阶段的最后一个残差结构的特征激活输出。将这些残差模块输出表示为{C2, C3, C4, C5}，对应于conv2，conv3，conv4和conv5的输出，并且注意它们相对于输入图像具有{4, 8, 16, 32}像素的步长。考虑到内存占用，没有将conv1包含在金字塔中。
自上而下的路径和横向连接
自上而下的路径（the top-down pathway ）是如何去结合低层高分辨率的特征呢？方法就是，把更抽象，语义更强的高层特征图进行上采样，然后把该特征横向连接（lateral connections）至前一层的特征，因此高层特征得到加强。值得注意的是，横向连接的两层特征在空间尺寸上要相同，这样做主要是为了利用底层的定位细节信息。
如图（d）所示，把高层特征做2倍上采样（最近邻上采样），然后将其和对应的前一层特征结合（前一层要经过$1\times 1$的卷积核才能用，目的是改变channels,使之和后一层的channels相同），结合方式就是element-wise相加的操作。重复迭代该过程，直至生成$1\times 1$最精细的特征图。迭代开始阶段，作者在C5层后面加了一个$1\times 1$的卷积核来产生最粗略的特征图，最后，作者用$3\times 3$的卷积核去处理已经融合的特征图（为了消除上采样的混叠效应），以生成最后需要的特征图。{C2, C3, C4, C5}层对应的融合特征层为{P2, P3, P4, P5}，对应的层空间尺寸是相通的。
FPN的优点：
1）低层的特征经过卷积和高层的信息上采样之后进行融合，在卷积神经网络中高层的特征具有较强的语义信息，低层的特征具有结构信息，将高层和低层的信息进行结合，是可以增强特征的表达能力。2）将候选框产生和提取特征的位置分散到特征金字塔的每一层，这样可以增加小目标特征映射的分辨率，对最后的预测是有好处的。

Retinanet

基于深度学习的目标检测算法有两类经典的结构：Two Stage 和 One Stage。
Two Stage：例如Faster-RCNN算法。第一级专注于proposal的提取，第二级对提取出的proposal进行分类和精确坐标回归。两级结构准确度较高，但因为第二级需要单独对每个proposal进行分类/回归，速度上就变慢。
One Stage：例如SSD，YOLO算法。此类算法摒弃了提取proposal的过程，只用一级就完成了识别/回归，虽然速度较快但准确率远远比不上两级结构。
产生精度差异的主要原因：类别失衡（Class Imbalance）。One Stage方法在得到特征图后，会产生密集的目标候选区域，而这些大量的候选区域中只有很少一部分是真正的目标，这样就造成了机器学习中经典的训练样本正负不平衡的问题。它往往会造成最终算出的training loss为占绝大多数但包含信息量却很少的负样本所支配，少样正样本提供的关键信息却不能在一般所用的training loss中发挥正常作用，从而无法得出一个能对模型训练提供正确指导的loss（而Two Stage方法得到proposal后，其候选区域要远远小于One Stage产生的候选区域，因此不会产生严重的类别失衡问题）。常用的解决此问题的方法就是负样本挖掘，或其它更复杂的用于过滤负样本从而使正负样本数维持一定比率的样本取样方法。该论文中提出了Focal Loss来对最终的Loss进行校正。
Focal Loss的目的：消除类别不平衡 + 挖掘难分样本
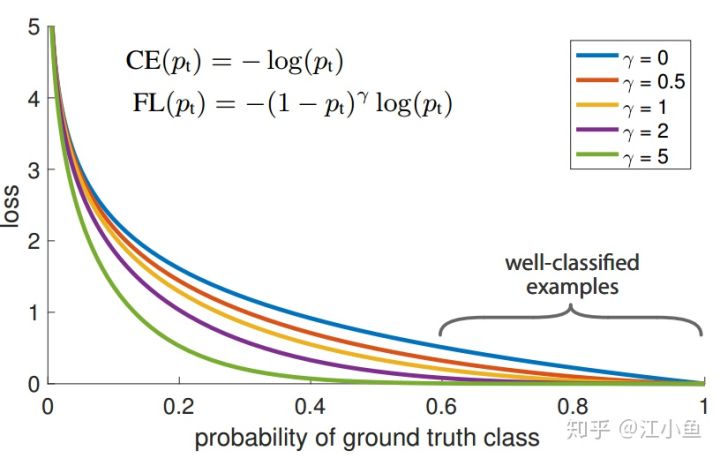
Focal Loss非常简单，就是在原有的交叉熵损失函数上增加了一个因子，让损失函数更加关注hard examples，以下是用于二值分类的交叉熵损失函数。其中$y\in{\pm1}$为类别真实标签，$p\in[0,1]$是模型预测的$y=1$的概率。

$$CE(p,y)= \begin{cases} -log(p) & if\ y=1 \\ -log(1-p) & otherwise \end{cases}$$

可以进行如下定义：

$$p_t= \begin{cases} p & if\ y=1 \\ 1-p & otherwise \end{cases}$$

因此交叉熵可以写成如下形式，即如下loss曲线图中蓝色曲线所示，可以认为当模型预测得到的$p_t\ge 0.6$的样本为容易分类的样本，而$p_t$值预测较小的样本为hard examples，最后整个网络的loss就是所有训练样本经过模型预测得到的值的累加，因为hard examples通常为少数样本，所以虽然其对应的loss值较高，但是最后全部累加后，大部分的loss值来自于容易分类的样本，这样在模型优化的过程中就会将更多的优化放到容易分类的样本中，而忽略hard examples。

$$CE(p,y)=CE(p_t)=-log(p_t)$$

对于这种类别不均衡问题常用的方法是引入一个权重因子$\alpha$，对于类别1的使用权重$\alpha$，对于类别-1使用权重$1-\alpha$，公式如下所示。但采用这种加权方式可以平衡正负样本的重要性，但无法区分容易分类的样本与难分类的样本。

$$CE(p_t)=-\alpha_tlog(p_t)$$

因此论文中提出在交叉熵前增加一个调节因子$(1-p_t)^{\gamma}$，其中$\gamma$为focusing parameter，且$\gamma \ge 0$，其公式变为如下，当$\gamma$取不同数值时loss曲线如图1所示。通过图中可以看到，当$\gamma$越来越大时，loss函数在容易分类的部分其loss几乎为零，而$p_t$较小的部分（hard examples部分）loss值仍然较大，这样就可以保证在类别不平衡较大时，累加样本loss，可以让hard examples贡献更多的loss，从而可以在训练时给与hard examples部分更多的优化。

$$FL(p_t)=-(1-p_t)^{\gamma}log(p_t)$$

在实际使用时，论文中提出在上述公式的基础上，增加一个$\alpha$平衡因子，可以产生一个轻微的精度提升，公式如下所示。

$$CE(p_t)=-\alpha_t(1-p_t)^{\gamma}log(p_t)$$

下图是RetinaNet的网络结构，整个网络相对Faster-RCNN简单了很多，主要由ResNet+FPN+2xFCN子网络构成。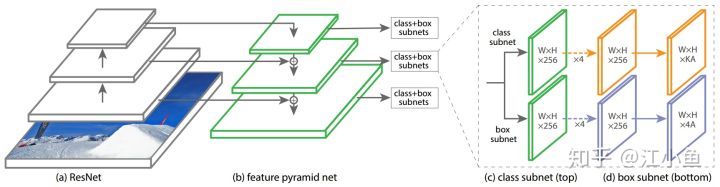

首先RetinaNet的Backbone是由ResNet+FPN构成，输入图像经过Backbone的特征提取后，可以得到$P_3~P_7$特征图金字塔，其中下标$l$表示特征金字塔的层数（$P_l$特征图的分辨率比输入图像小$2^l$），得到的特征金字塔的每层$C=256$通道。
在得到特征金字塔后，对每层特征金字塔分别使用两个子网络（分类网络+检测框位置回归）。这两个子网络由RPN网络修改得到。
与RPN网络类似，也使用anchors来产生proposals。特征金字塔的每层对应一个anchor面积，为了产生更加密集的coverage，增加了三个面积比例$\begin{Bmatrix}2^0,2^{\frac{1}{2}},2^{\frac{2}{3}} \end{Bmatrix}$（即使用当前anchor对应的面积分别乘以相应的比例，形成三个尺度），然后anchors的长宽比仍为$\begin{Bmatrix}1:2,1:1,2:1 \end{Bmatrix}$，因此特征金字塔的每一层对应A = 9种Anchors。原始RPN网络的分类网络只是区分前景与背景两类，此处将其改为目标类别的个数K。
特征金字塔每层都相应的产生目标类别与位置的预测，最后再将其融合起来，同时使用NMS来得到最后的检测结果。

Faster R-CNN+FPN+Focal loss

Faster R-CNN+FPN结合细节
代码
网络结构
优化方案

YOLO

算法特点：1）将物体检测作为回归问题求解。基于一个单独的End-To-End网络，完成从原始图像的输入到物体位置和类别的输出，输入图像经过一次Inference，便能得到图像中所有物体的位置和其所属类别及相应的置信概率。2）YOLO网络借鉴GoogleNet网络结构，不同的是，YOLO未使用Inception Module，而是使用$1\times 1$卷积层（此处$1\times 1$卷积层的存在是为了跨通道信息整合）+ $3\times 3$卷积层简单代替。3）Fast YOLO使用9个卷积层代替YOLO的24个，网络更轻快，速度从YOLO的45fps提升到155fps，但是同时损失了检测准确率。4）使用全图作为Context信息，背景错误（把背景错认为物体）比较少。5）泛化能力强。在自然图像上训练好的结果在艺术作品中依然具有很好的效果。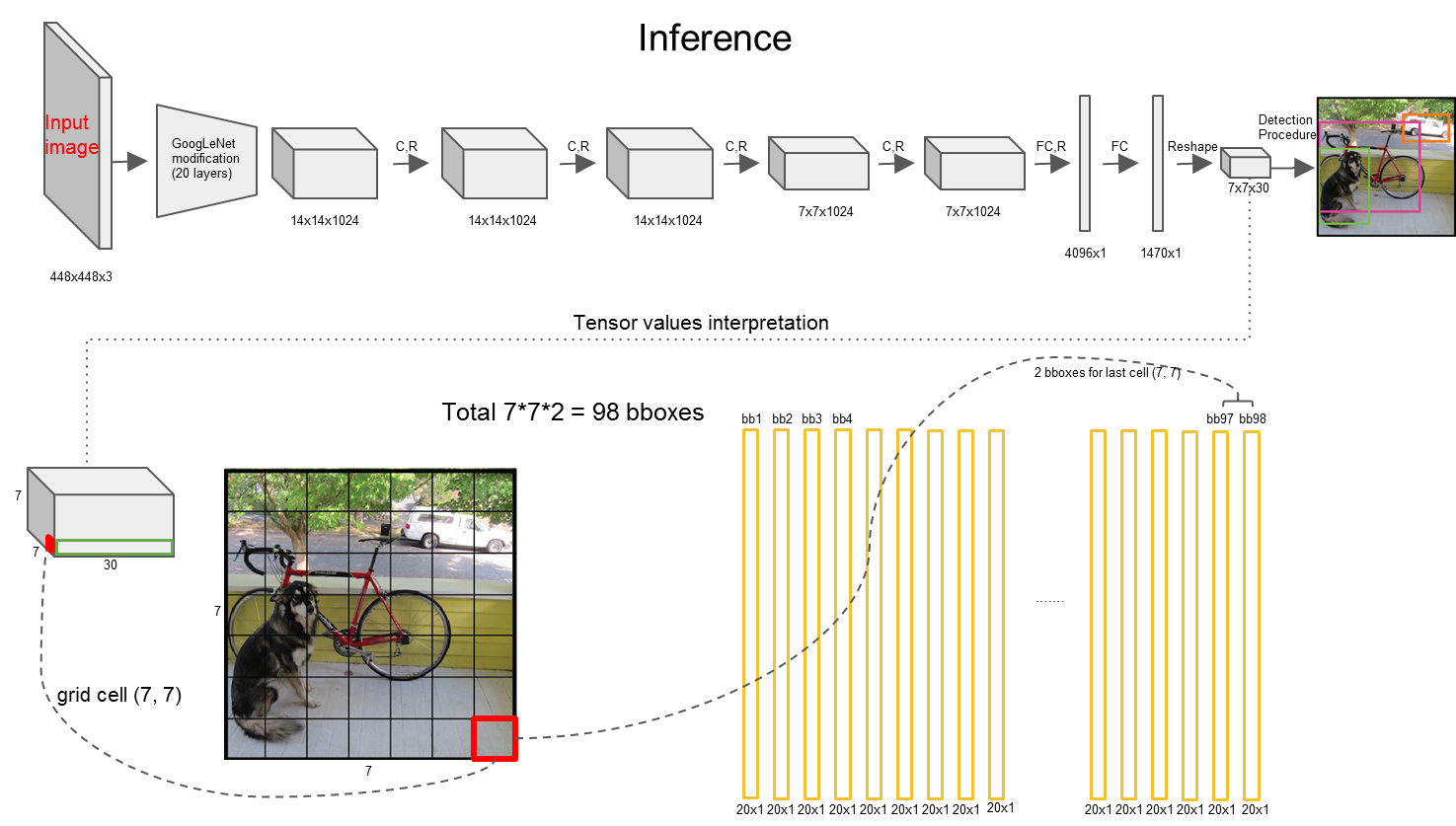

一、大致流程
1）对于一个输入图像，首先将图像划分成$7\times 7$的网络。
2）对于每个网格，我们都预测2个边框（包括每个边框是目标的置信度以及每个边框区域在多个类别上的概率）。
3）根据上一步可以预测出$7\times 7\times 2$个目标窗口，然后根据阈值去除可能性比较低的目标窗口，最后NMS去除冗余窗口即可。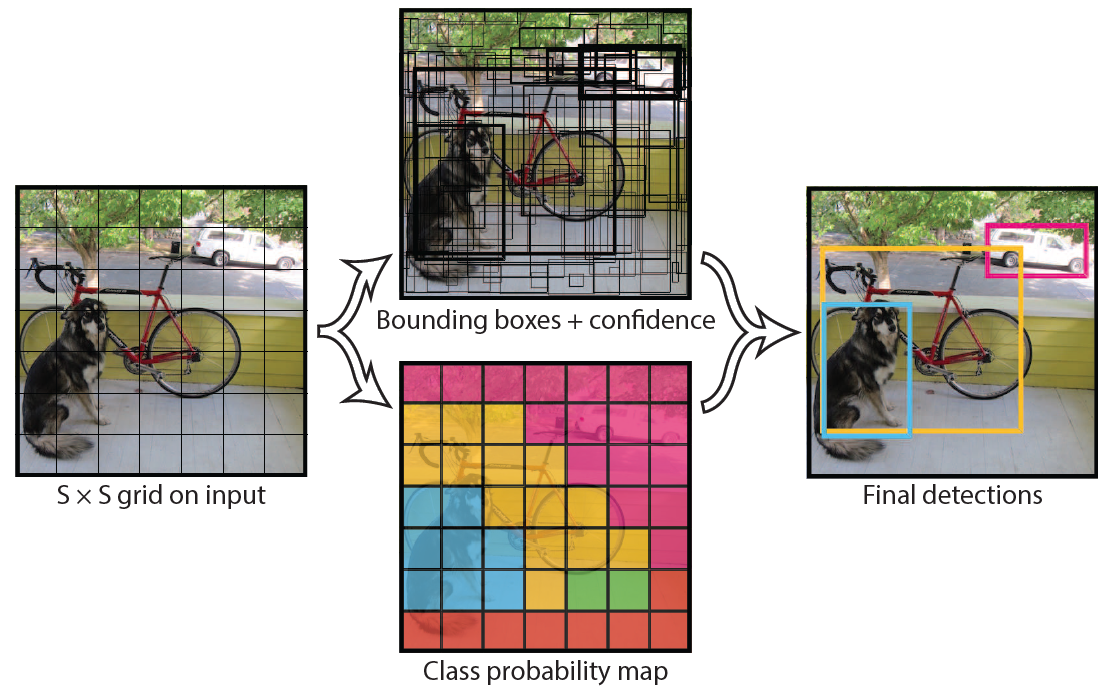

二、训练
1）预训练分类网络：在ImageNet 1000-class Competition Dataset预训练一个分类网络，这个网络时前文网络结构中前20个卷积网络+Average-Pooling Layer+Fully Connected Layer(此时网络的输入是$224\times 224$)。
2）训练检测网络：在预训练网络中增加卷积和全连接层可以改善性能。YOLO添加4个卷积层和2个全连接层，随机初始化权重。检测要求细粒度的视觉信息，所以把网络输入也从$224\times 224$变成$448\times 448$。一幅图像分成$7\times 7$个网格，某个物体的中心落在这个网格中此网络就负责预测这个物体。每个网络预测两个Bounding Box。网格负责类别信息，Bounding Box负责坐标信息（4个坐标信息及一个置信度），所以最后一层输出为$7\times 7\times (2\times (4+1) + 20) = 7\times 7\times 30$的维度。Bounding Box的坐标使用图像的大小进行归一化0-1，Confidence使用$Pr(Object) * IOU{pred}^{truth}$计算，其中第一项表示是否有物体落在网格中，第二项表示预测的框和实际的框之间的IOU值。
3）损失函数的确定：损失函数的定义如下，损失函数的设计目标就是让坐标，置信度和类别这三个方面达到很好的平和。简单地全部采用Sum-Squared Error Loss来做这件事会有以下不足：a)8维的Localization Error和20维的Classification Error同等重要显然是不合理的；b)如果一个网格中没有Object（一幅图中这种玩个很多），那么就会将这些网络中的Box的COnfidence降低到0，相对于较少的有Object的网络，这种做法是Overpowering的，这会导致网络不稳定甚至发散。解决方案如下：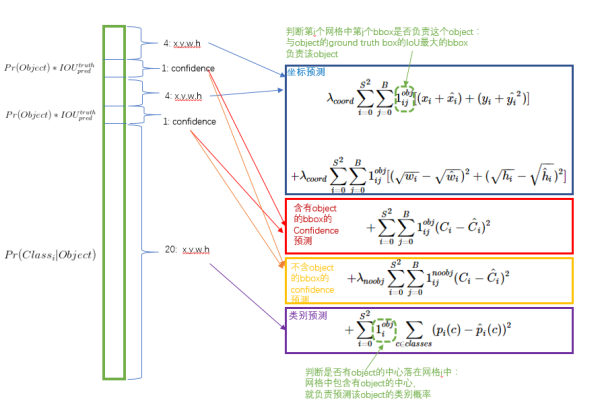

首先更重视8维的坐标预测，给这些损失前面赋予更大的Loss Weight，记为$\lambda{coord}$，在Pascal VOC训练中取5（上图蓝色框）。对于没有Object的Bbox的Confidence Loss，赋予小的Loss Weight，记为$\lambda{noobj}$，在Pascal VOC训练中取0.5（上图橙色框）。有Object的Bbox的Confidence Loss（上图红色框）和类别的Loss（上图紫色框）的Loss Weight正常取1。对于不同大小的Bbox预测中，相比于大Bbox预测偏一点，小Bbox预测偏一点更不能忍受。而Sum-Square Error Loss中对同样的偏移Loss是一样的。为了缓和这个问题，将Bbox的Width和Height取平方根代替原本的Height和Width。如下图所示：Small Bbox的横轴值较小，发生偏移时，反应到y轴上的Loss(下图绿色)比Big Bbox(下图红色)要大。一个网格预测多个Bbox，在训练时我们希望每个Object（Ground True box）只有一个Bbox专门负责（一个Object一个Bbox）。具体做法是与Ground True Box(Object)的IOU最大的Bbox负责该Ground True Box(Object)的预测。这种做法称作Bbox Predictor的Specialization（专职化）。每个预测器会对特定（Size,Aspect Ratio or Classed of Object）的Ground True Box预测的越来越好。
三、测试
1）计算每个Bbox的Class-Specific Confidence Score:每个网格预测的Class信息($Pr(Classi|Object)$)和Bbox预测的Confidence信息($Pr(Object)\times IOU{pred}^{truth}$)相乘，就得到每个Bbox的Class-Specific Confidence Score。

$$Pr(Class_i|Object)\times Pr(Object)\times IOU_{pred}^{truth}=Pr(Class_i)\times IOU_{pred}^{truth}$$

2）进行Non-Maximum Suppression(NMS)：得到每个Bbox的Class-Specific Confidence Score以后，设置阈值，滤掉得分低的Bboxes，对保留的Bboxes进行NMS处理就得到最终的检测结果。
四、存在问题
1）YOLO对相互靠的很近的物体（挨在一起且中点都落在同一个格子上的情况），还有很小的群体检测效果不好，这是因为一个网络中只预测了两个框，并且只属于一类。
2）测试图像中，当同一类物体出现的不常见的长宽比和其他情况时泛化能力偏弱。
3）由于损失函数的问题，定位误差是影响检测效果的主要原因，尤其是大小物体的处理上，还有待加强。

YOLOV2、YOLOV3

YOLOV2/YOLO9000 更准、更快、更强

YOLO v1对于bounding box的定位不是很好，在精度上比同类网络还有一定的差距。作者希望改进的方向是改善 recall，提升定位的准确度，同时保持分类的准确度。YOLO V2在V1基础上做出改进：
1）受到Faster RCNN方法的启发，引入了anchor。使用了K-Means方法，对anchor数量进行了讨论。
2）修改了网络结构，去掉了全连接层，改成了全卷积结构。
3）训练时引入了世界树（WordTree）结构，将检测和分类问题做成了一个统一的框架，并且提出了一种层次性联合训练方法，将ImageNet分类数据集和COCO检测数据集同时对模型训练。
更准
Batch Normalization
使用 Batch Normalization 对网络进行优化，让网络提高了收敛性，同时还消除了对其他形式的正则化（regularization）的依赖。通过对 YOLO 的每一个卷积层增加 Batch Normalization，最终使得 mAP 提高了2%，同时还使模型正则化。使用 Batch Normalization 可以从模型中去掉 Dropout，而不会产生过拟合。
High resolution classifier
目前业界标准的检测方法，都要先把分类器（classifier）放在ImageNet上进行预训练。从 Alexnet 开始，大多数的分类器都运行在小于 $256\times 256$ 的图片上。而现在 YOLO 从 $224\times 224$ 增加到了 $448\times 448$，这就意味着网络需要适应新的输入分辨率。
为了适应新的分辨率，YOLO v2 的分类网络以 $448\times 448$ 的分辨率先在 ImageNet上进行微调，微调 10 个 epochs，让网络有时间调整滤波器（filters），好让其能更好的运行在新分辨率上，还需要调优用于检测的 Resulting Network。最终通过使用高分辨率，mAP 提升了4%。
Convolution with anchor boxes
YOLOV1包含有全连接层，从而能直接预测 Bounding Boxes 的坐标值。 Faster R-CNN 的方法只用卷积层与 Region Proposal Network 来预测 Anchor Box 偏移值与置信度，而不是直接预测坐标值。作者发现通过预测偏移量而不是坐标值能够简化问题，让神经网络学习起来更容易。
收缩网络让其运行在 $416\times 416$ 而不是 $448\times 448$。由于图片中的物体都倾向于出现在图片的中心位置，特别是那种比较大的物体，所以有一个单独位于物体中心的位置用于预测这些物体。YOLO 的卷积层采用 32 这个值来下采样图片，所以通过选择 $416\times 416$ 用作输入尺寸最终能输出一个 $13\times 13$ 的特征图。 使用 Anchor Box 会让精确度稍微下降，但用了它能让 YOLO 能预测出大于一千个框，同时 recall 达到88%，mAP 达到 69.2%。
Dimension clusters
Anchor boxes的宽高维度往往是精选的先验框（hand-picked priors）也就是说人工选定的先验框。虽然在训练过程中网络也会学习调整框的宽高维度，最终得到准确的bounding boxes。但是，如果一开始就选择了更好的、更有代表性的先验框维度，那么网络就更容易学到准确的预测位置。为了优化，在训练集的 Bounding Boxes 上跑一下 k-means聚类，来找到一个比较好的值。
Fine-Grained Features
YOLOv1在对于大目标检测有很好的效果，但是对小目标检测上，效果欠佳。为了改善这一问题，作者参考了Faster R-CNN和SSD的想法，在不同层次的特征图上获取不同分辨率的特征。作者将上层的(前面26×26)高分辨率的特征图（feature map）直接连到13×13的feature map上。把26×26×512转换为13×13×2048，并拼接在一起使整体性能提升1%。
Multi-Scale Training
和GoogleNet训练时一样，为了提高模型的鲁棒性（robust），在训练的时候使用多尺度的输入进行训练。YOLOv2 每迭代几次都会改变网络参数。每 10 个 Batch，网络会随机地选择一个新的图片尺寸，由于使用了下采样参数是 32，所以不同的尺寸大小也选择为 32 的倍数 {320，352,…,608}，最小 320x320，最大 608x608，网络会自动改变尺寸，并继续训练的过程。
更快
大多数目标检测的框架是建立在VGG-16上的，VGG-16在ImageNet上能达到90%的top-5，但是单张图片需要30.69 billion 浮点运算，YOLO2是依赖于DarkNet-19的结构，该模型在ImageNet上能达到91%的top-5，并且单张图片只需要5.58 billion 浮点运算，大大的加快了运算速度。
YOLOv2去掉YOLOv1的全连接层，同时去掉YOLO v1的最后一个池化层，增加特征的分辨率，修改网络的输入，保证特征图有一个中心点，这样可提高效率。并且是以每个anchor box来预测物体种类的。
作者将分类和检测分开训练，在训练分类时，以Darknet-19为模型在ImageNet上用随机梯度下降法（Stochastic gradient descent）跑了160epochs，跑完了160 epochs后，把输入尺寸从224×224上调为448×448，这时候学习率调到0.001，再跑了10 epochs， DarkNet达到了top-1准确率76.5%，top-5准确率93.3%。
在训练检测时，作者把分类网络改成检测网络，去掉原先网络的最后一个卷积层，取而代之的是使用3个3×3x1024的卷积层，并且每个新增的卷积层后面接1×1的卷积层，数量是我们要检测的类的数量。
更强
论文提出了一种联合训练的机制：使用识别数据集训练模型识别相关部分，使用分类数据集训练模型分类相关部分。
众多周知，检测数据集的标注要比分类数据集打标签繁琐的多，所以ImageNet分类数据集比VOC等检测数据集高出几个数量级。所以在YOLOv1中，边界框的预测其实并不依赖于物体的标签，YOLOv2实现了在分类和检测数据集上的联合训练。对于检测数据集，可以用来学习预测物体的边界框、置信度以及为物体分类，而对于分类数据集可以仅用来学习分类，但是其可以大大扩充模型所能检测的物体种类。
作者选择在COCO和ImageNet数据集上进行联合训练，遇到的第一问题是两者的类别并不是完全互斥的，比如”Norfolk terrier”明显属于”dog”，所以作者提出了一种层级分类方法（Hierarchical classification），根据各个类别之间的从属关系（根据WordNet）建立一种树结构WordTree，结合COCO和ImageNet建立的词树（WordTree）如下图所示：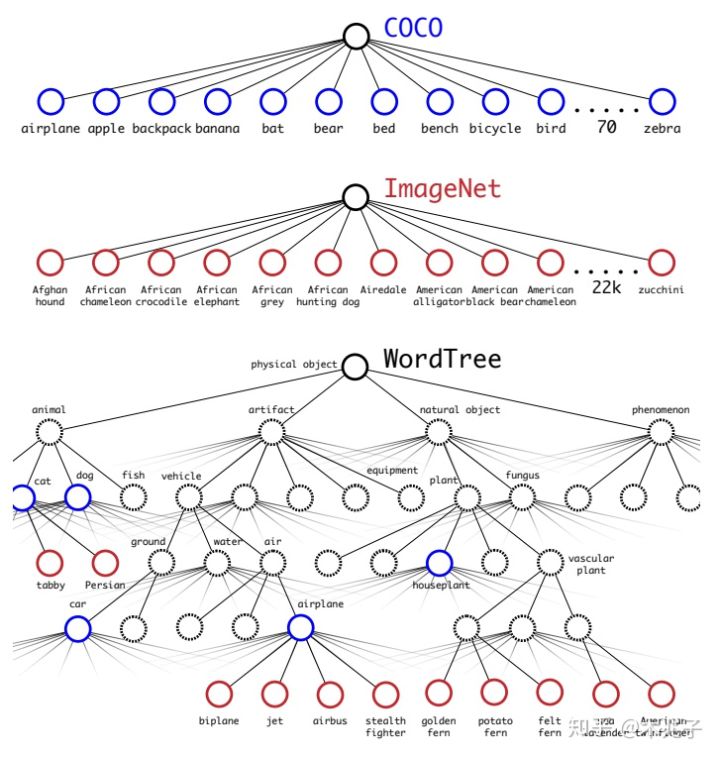

WordTree中的根节点为”physical object”，每个节点的子节点都属于同一子类，可以对它们进行softmax处理。在给出某个类别的预测概率时，需要找到其所在的位置，遍历这个路径，然后计算路径上各个节点的概率之积。
在训练时，如果是检测样本，按照YOLOv2的loss计算误差，而对于分类样本，只计算分类误差。在预测时，YOLOv2给出的置信度就是 ，同时会给出边界框位置以及一个树状概率图。在这个概率图中找到概率最高的路径，当达到某一个阈值时停止，就用当前节点表示预测的类别。

YOLOv3

改进之处：
1）多尺度预测
2）更好的基础网络（类ResNet）和分类器darknet-53
多尺度预测
原来的YOLO v2有一个层叫：passthrough layer，假设最后提取的feature map的size是$13\times 13$，那么这个层的作用就是将前面一层的$26\times 26$的feature map和本层的$13\times 13$的feature map进行连接，有点像ResNet。这样的操作也是为了加强YOLO算法对小目标检测的精确度。这个思想在YOLO v3中得到了进一步加强，在YOLO v3中采用类似FPN的上采样（upsample）和融合做法（最后融合了3个scale，其他两个scale的大小分别是$26\times 26$和$52\times 52$），在多个scale的feature map上做检测，对于小目标的检测效果提升还是比较明显的。虽然在YOLO v3中每个网格预测3个边界框，看起来比YOLO v2中每个grid cell预测5个边界框要少，但因为YOLO v3采用了多个尺度的特征融合，所以边界框的数量要比之前多很多。
darknet-53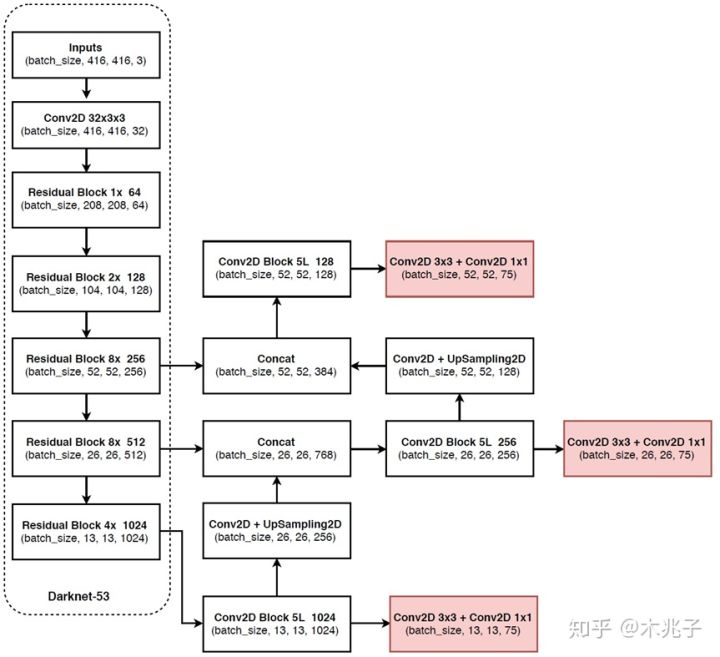

SSD

SSD模型
算法特点
1）SSD结合了YOLO中的回归思想和Faster R-CNN中的Anchor机制，使用全图各个位置的尺度区域特征进行回归，既保持了YOLO速度快的特性，也保证了窗口预测的跟Faster-RCNN一样比较精准。
2）SSD的核心是在特征图上采用卷积核来预测一系列Default Bounding Boxes的类别、坐标偏移。为了提高检测准确率，SSD在不同尺度的特征图上进行预测。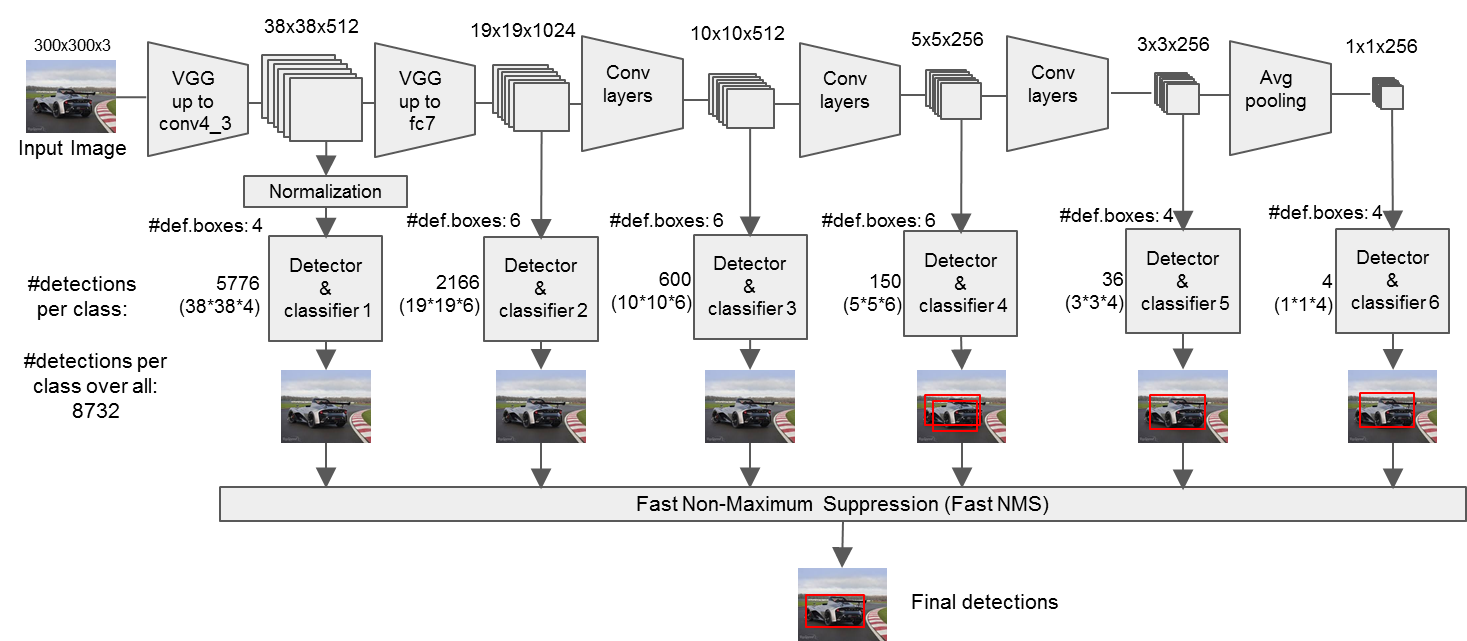

一、模型结构
1、多尺度特征图（Multi-scale Feature Map For Detection）
在图像Base Network基础上，将Fc6，Fc7变为Conv6，Conv7两个卷积层，添加了一些卷积层（Conv8,Conv9,Conv10,Conv11），这些层的大小逐渐减小，可以进行多尺度预测。
2、卷积预测器（Convolutional Predictors For Detection）
每个新添加的卷积层和之前的部分卷积层，使用一系列的卷积核进行预测。对于一个大小为$m\times n$，$p$通道的卷积层，使用$3\times 3$的$p$通道卷积核作为基础预测元素进行预测，在某个位置上预测出一个值，该值可以是某一类别的得分，也可是相对于Default Bounding Boxes的偏移量，并且在图像中每个位置都将产生一个值。
3、默认框和比例（Default Boxes And Aspect Ratio）
在特征图的每个位置预测K个Box，对于每个Box，预测C个类别得分，以及相对于Default Bounding Box的4个偏移值，这样需要$(C+4)\times k$个预测器，在$m\times n$的特征图上将产生$(C+4)\times k\times m\times n$个预测值。这里，Default Bounding Box类似于Faster R-CNN中Anchor是，下图所示。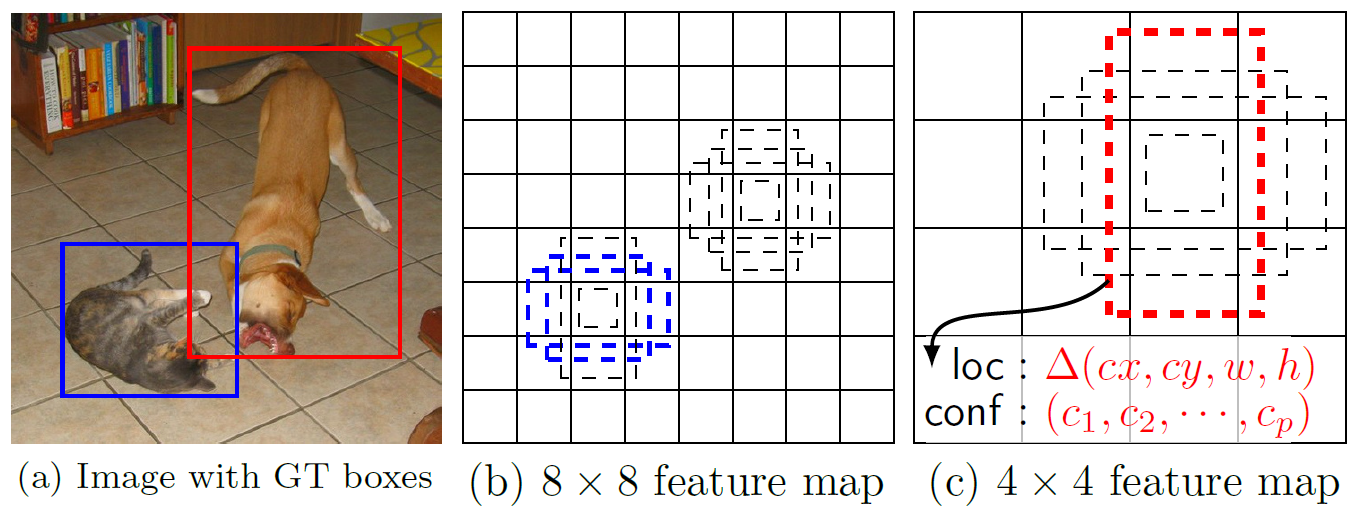

二、模型训练
1、监督学习的训练关键是人工标注的label，对于包含Default Box（在Faster R-CNN中叫做Anchor）的网络模型（如:YOLO,Faster R-CNN,MultiBox）关键点就是如何把标注信息（Ground True Box,Ground True Category）映射到（Default Box）上。
2、给定输入图像以及每个物体的Ground Truth，首先找到每个Ground True Box对应的Default Box中IOU最大的作为正样本。然后，在剩下的Default Box中找到那些与任意一个Ground truth Box的IOU大于0.5的Default Box作为正样本。其他的作为负样本（每个Default Box要么是正样本Box要么是负样本Box）。如上图中，两个Default Box与猫匹配，一个与狗匹配。在训练过程中，采用Hard Negative Mining 的策略（根据Confidence Loss对所有的Box进行排序，使正负例的比例保持在1:3） 来平衡正负样本的比率。
3、损失函数
与Faster-RCNN中的RPN是一样的，不过RPN是预测Box里面有Object或者没有，没有分类，SSD直接用的Softmax分类。Location的损失，还是一样，都是用Predict box和Default Box/Anchor的差 与Ground Truth Box和Default Box/Anchor的差进行对比，求损失。

其中，$x{i,j}^p=1$表示 第i个Default Box与类别p的第j个Ground Truth Box相匹配，否则若不匹配的话，则$x{i,j}^p=0$
4、Default Box的生成
对每一张特征图，按照不同的大小（Scale） 和长宽比（Ratio）生成生成k个默认框（Default Boxes）。
（1）Scale：每一个Feature Map中Default Box的尺寸大小计算如下：

$$s_k=s_{min}+\frac{s_{max}-s_{min}}{m-1}(k-1), \quad k\in [1, m]$$

其中，$S{min}$取值0.2，$s{max}$取值0.95，意味着最低层的尺度是0.2，最高层的尺度是0.95。
（2）Ratio：使用不同的Ratio值$a_=1,2,3,\frac{1}{2},\frac{1}{3}$计算Default Box的宽度和高度：$w_k^a=s_k\sqrt{a_r},h_k^a=s_k/\sqrt{a_r}$。另外对于Ratio=1的情况，还增加了一个Default Box，这个Box的Scale为$s’_k=\sqrt{s_ks_k+1}$。也就是总共有6种不同的Default Box。
（3）Default Box中心：每个Default Box的中心位置设置成$(\frac{i+0.5}{|f_k|},\frac{j+0.5}{|f_k|})$，其中$|f_k|$表示第k个特征图的大小$i,j\in[0,|f_k|]$。
5）Data Augmentation：为了模型更加鲁棒，需要使用不同尺寸的输入和形状，作者对数据进行了多种方式的随机采样。

mobile net

图像分割

FCN

UNet

目标追踪

多目标跟踪介绍

多目标跟踪，即MOT（Multi-Object Tracking），顾名思义，就是在一段视频中同时跟踪多个目标。MOT主要应用场景是安防监控和自动驾驶等，这些场景中我们往往需要对众多目标同时进行追踪。
而由于是多目标，自然就会产生新目标进入与旧目标消失的问题，这就是与单目标跟踪算法区别最大的一点。而由于这一点区别，也就导致跟踪策略的不同。在单目标跟踪中，我们往往会使用给定的初始框，在后续视频帧中对初始框内的物体进行位置预测。而多目标跟踪算法，大部分都是不考虑初始框的，原因就是上面的目标消失与产生问题。取而代之，在多目标跟踪领域常用的跟踪策略是TBD（Tracking-by-Detecton），又或者也可叫DBT（Detection-Based-Tracking）。即在每一帧进行目标检测，再利用目标检测的结果来进行目标跟踪，这一步我们一般称之为数据关联（Data Assoiation）。
这里自然引出了多目标跟踪算法的一种分类：TBD（Tracking-by-Detecton）与DFT（Detection-Free Tracking），也即基于检测的多目标跟踪与基于初始框无需检测器的多目标跟踪。基于初始化帧的跟踪，在视频第一帧中选择你的目标，之后交给跟踪算法去实现目标的跟踪。这种方式基本上只能跟踪你第一帧选中的目标，如果后续帧中出现了新的物体目标，算法是跟踪不到的。这种方式的优点是速度相对较快。缺点很明显，不能跟踪新出现的目标。基于目标检测的跟踪，在视频每帧中先检测出来所有感兴趣的目标物体，然后将其与前一帧中检测出来的目标进行关联来实现跟踪的效果。这种方式的优点是可以在整个视频中跟踪随时出现的新目标。TBD则是目前学界业界研究的主流。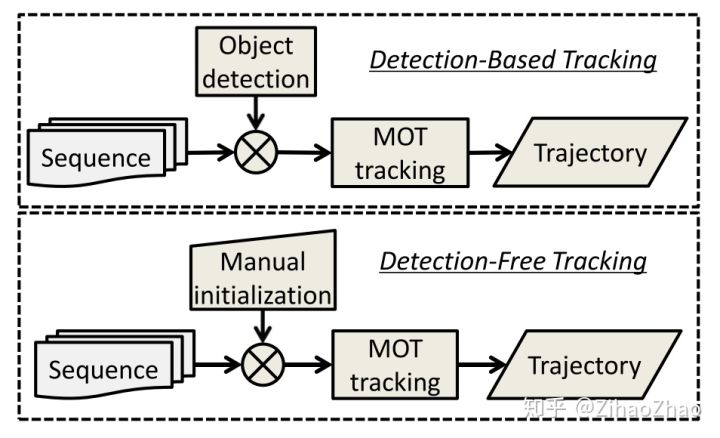

不得不提的是另一种多目标跟踪算法的分类方式：在线跟踪（Online）与离线跟踪（Offline）。上文提到，大家往往会使用数据关联来进行多目标跟踪。而数据关联的效果，与你能使用的数据是有着直接的关系的。在Online跟踪中，我们只能使用当前帧及之前帧的信息来进行当前帧的跟踪。而在Offline跟踪中则没有了这个限制，我们对每一帧的预测，都可以使用整个视频的信息，这样更容易获得一个全局最优解。两种方式各有优劣，一般视应用场合而定，Offline算法的效果一般会优于Online算法。而介于这两者之间，还有一种称之为Near-Online的跟踪方式，即可以部分利用未来帧的信息。下图形象解释了Online与Offline跟踪的区别。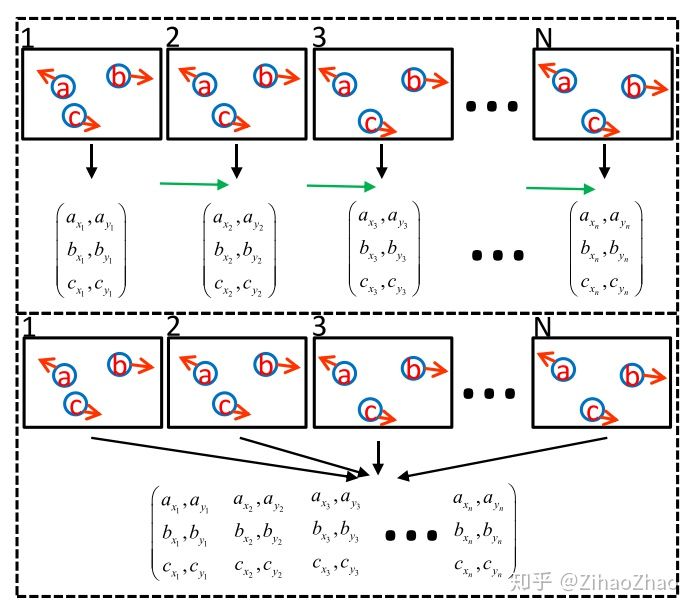

评价指标

Trajectory（轨迹）：一条轨迹对应这一目标在一段时间内的位置序列。
Tracklet（轨迹段）：形成Trajectory过程中的轨迹片段。完整的Trajectory是由属于同一物理目标的Tracklets构成。
ID switch（ID 切换）：又称ID sw.。对于同一个目标，由于跟踪算法误判，导致其ID发生切换的次数。跟踪算法中理想的ID switch应该为0.
对于多目标跟踪，最主要的评价指标就是MOTA。这个指标综合了三点因素：FP、FN、IDsw.。FP即False Postive，为误检测的目标数量；FN即False Negetive，为未检出的真实目标数量；IDsw.即同一目标发生ID切换的次数。

$$MOTA=1-\frac{(FN+FP+IDSW)}{GT}\ \in(-\infty,1]$$ $$MOTP=\frac{\sum_{t,i}d_{t,i}}{\sum_tc_t}$$

其中$ct$表示帧t中的匹配数，并且$d{t,i}$是假设i与分配的真实对象之间的边界框重叠。此度量标准很少考虑有关跟踪的信息，而侧重于检测的质量。

SORT

现在多目标跟踪算法的效果，与目标检测的结果息息相关。在实际工程中，为了提高多目标跟踪的效果，可以从检测器入手，跟踪效果也会水涨船高。
SORT采用的是在线跟踪的方式，不使用未来帧的信息。在保持100fps以上的帧率的同时，也获得了较高的MOTA（在当时16年的结果中）。
多目标跟踪中SORT算法思想理解流程：
在跟踪之前，对所有目标已经完成检测，实现了特征建模过程。
1）对第一帧使用目标检测模型进行目标检测，得到第一帧中所有目标的分类和位置（假设有M个目标），并标注一个独有id。对每个目标初始化卡尔曼滤波跟踪器，预测每个目标在下一帧的位置；
2）对第二帧使用目标检测模型进行目标检测，得到第二帧中所有目标的分类和位置（假设有N个目标），求第一帧M个目标和第二帧N个目标两两目标之间的IOU，建立代价矩阵，使用匈牙利匹配算法得到IOU最大的唯一匹配（数据关联部分），再去掉匹配值小于iou_threshold的匹配对；
3）用第二帧中匹配到的目标的位置去更新卡尔曼跟踪器，计算第二帧时的卡尔曼增益Kk，状态估计值xk，估计误差协方差Pk。并输出状态估计值xk用来计算下一帧中的预测位置。对于本帧中没有匹配到的目标重新初始化卡尔曼滤波跟踪器；
后面每一帧图像都按第一帧和第二帧的做法进行类似处理即可。其中，卡尔曼跟踪器联合了历史跟踪记录，调节历史box与本帧box的残差，更好的匹配跟踪id。
匈牙利算法是一种寻找二分图的最大匹配的算法，在多目标跟踪问题中可以简单理解为寻找前后两帧的若干目标的匹配最优解的一种算法。而卡尔曼滤波可以看作是一种运动模型，用来对目标的轨迹进行预测，并且使用确信度较高的跟踪结果进行预测结果的修正。
SORT在以往二阶段匹配算法的基础上进行了创新。以往二阶段匹配算法是先使用匈牙利算法对相邻帧之间的目标进行匹配生成很多tracklets，之后使用这些tracklets进行二次匹配，以解决遮挡等问题引起的轨迹中断。但这种二阶段匹配方式弊端也很明显，因为这种方式先天地要求必须以Offline的方法进行跟踪，而无法做到Online。SORT将这种二阶段匹配算法改进为了一阶段方法，并且可以在线跟踪。具体而言，SORT引入了线性速度模型与卡尔曼滤波来进行位置预测，在无合适匹配检测框的情况下，使用运动模型来预测物体的位置。在数据关联的阶段，SORT使用的依旧是匈牙利算法逐帧关联，不过作者还引入了IOU（Intersection-Over-Union）距离。不过SORT用的是带权重的匈牙利算法，其实就是KM算法，用IOU距离作为权重（也叫cost矩阵）。作者代码里是直接用sklearn的linear_assignment实现。并且当IOU小于一定数值时，不认为是同一个目标，理论基础是视频中两帧之间物体移动不会过多。作者在代码中选取的阈值是0.3。
预测模型（卡尔曼滤波器）
作者近似地认为目标的不同帧间地运动是和其他物体及相机运动无关的线性运动。每一个目标的状态可以表示为：

$$x=[u,v,s,r,\dot u,\dot v,\dot s]^T$$

其中u和v分别代表目标的中心坐标，而s和r分别代表目标边界框的比例（面积）和长宽比，长宽比被认为是常数，需要保持不变。
当进行目标关联时，使用卡尔曼滤波器，用上一帧中目标的位置信息预测下一帧中这个目标的位置。若上一帧中没有检测到下一帧中的某个目标，则对于这个目标，重新初始化一个新的卡尔曼滤波器。关联完成后，使用新关联的下一帧中该目标的位置来更新卡尔曼滤波器。
数据关联（匈牙利匹配）
SORT算法中的代价矩阵为上一帧的M个目标与下一帧的N个目标两两目标之间的IOU。当然，小于指定IOU阈值的指派结果是无效的（源码中阈值设置为0.3）。
此外，作者发现使用IOU能够解决目标的短时被遮挡问题。这是因为目标被遮挡时，检测到了遮挡物，没有检测到原有目标，假设把遮挡物和原有目标进行了关联。那么在遮挡结束后，因为在相近大小的目标IOU往往较大，因此很快就可以恢复正确的关联。这是建立在遮挡物面积大于目标的基础上的。

deep SORT

之前的SORT算法使用简单的卡尔曼滤波处理逐帧数据的关联性以及使用匈牙利算法进行关联度量，这种简单的算法在高帧速率下获得了良好的性能。但由于SORT忽略了被检测物体的表面特征，因此只有在物体状态估计不确定性较低是才会准确，在Deep SORT中，我们使用更加可靠的度量来代替关联度量，并使用CNN网络在大规模行人数据集进行训练，并提取特征，已增加网络对遗失和障碍的鲁棒性。
状态估计
使用一个8维空间去刻画轨迹在某时刻的状态：

$$(u,v,\gamma,h,\dot x,\dot y,\dot\gamma,\dot h)$$

使用一个kalman滤波器预测更新轨迹，该卡尔曼滤波器采用匀速模型和线性观测模型。通过卡尔曼估计对u,v,r,h进行估计，u，v是物体中心点的位置，r是长宽比，h是高。运动估计对于运动状态变化不是很剧烈和频繁的物体能取得比较好的效果。其观测变量为：

$$(u,v,\gamma,h)$$

轨迹处理
对于每一个追踪目标，都有一个阈值ak用于记录轨迹从上一次成功匹配到当前时刻的时间（即连续没有匹配的帧数），我们称之为轨迹。当该值大于提前设定的阈值Amax则认为该轨迹终止，直观上说就是长时间匹配不上的轨迹则认为该轨迹已经结束。
在匹配时，对于没有匹配成功的目标都认为可能产生新的轨迹。但由于这些检测结果可能是一些错误警告，所以对这种情形新生成的轨迹标注状态’tentative’，然后观查在接下来的连续若干帧（论文中是3帧）中是否连续匹配成功，是的话则认为是新轨迹产生，标注为’confirmed’，否则则认为是假性轨迹,状态标注为’deleted’。
分配问题
在SORT中，我们直接使用匈牙利算法去解决预测的Kalman状态和新来的状态之间的关联度，现在我们需要将目标运动和表面特征信息相结合，通过融合这两个相似的测量指标。
Motion Metric
使用马氏距离来评测预测的Kalman状态和新来的状态：

$$d^{(1)}(i,j)=(d_j-y_i)^TS_i^{-1}(d_j-y_i)$$

表示第j个detection和第i条轨迹之间的运动匹配度，其中$S_i$是轨迹由kalman滤波器预测得到的在当前时刻观测空间的协方差矩阵， $y_i$是轨迹在当前时刻的预测观测量， $d_i$时第j个detection的状态$(u,v,r,h)$
考虑到运动的连续性，可以通过该马氏距离对detections进行筛选，文中使用卡方分布的0.95分位点作为阈值$ t^(1)=0.4877$,我们可以定义一个门限函数。

$$b_{i,j}^{(1)}=\mathbf{1}[d^{(1)}(i,j)\leq t^{(1)}]$$

Appearance Metric
当目标运动不确定性较低时，马氏距离是一个很好的关联度量，但在实际中，如相机运动时会造成马氏距离大量不能匹配，也就会使这个度量失效，因此，我们整合第二个度量标准，对每一个BBox检测框$dj$我们计算一个表面特征描述子 $r_j,|r_j|=1$ , 我们会创建一个gallery用来存放最新的$L_k=100$个轨迹的描述子，即$R_k=\begin{Bmatrix}r_k^{(i)}\end{Bmatrix}{k=1}^{L_k}$，然后我们使用第i个轨迹和第j个轨迹的最小余弦距离作为第二个衡量尺度！

$$d^(2)(i,j)=min{1-r_j^Tr_k^{(i)}|r_k^(i)\in R_i}$$

当然，我们也可以用一个门限函数来表示

$$b_{i,j}^{(2)}=\mathbf{d^{(2)}(i,j)\le t^{(2)}}$$

接着，我们把这两个尺度相融合为：

$$c_{i,j}=\lambda d^{(1)}(i,j)+(1-\lambda)d^{(2)}(i,j)$$ $$b_{i,j}=\prod_{m=1}^2b_{i,j}^{(m)}$$

总之，距离度量对于短期的预测和匹配效果很好，而表观信息对于长时间丢失的轨迹而言，匹配度度量的比较有效。超参数的选择要看具体的数据集，比如文中说对于相机运动幅度较大的数据集，直接不考虑运动匹配程度。
级联匹配
如果一条轨迹被遮挡了一段较长的时间，那么在kalman滤波器的不断预测中就会导致概率弥散。那么假设现在有两条轨迹竞争同一个目标，那么那条遮挡时间长的往往得到马氏距离更小，使目标倾向于匹配给丢失时间更长的轨迹，但是直观上，该目标应该匹配给时间上最近的轨迹。
导致这种现象的原因正是由于kalman滤波器连续预测没法更新导致的概率弥散。假设本来协方差矩阵是一个正态分布，那么连续的预测不更新就会导致这个正态分布的方差越来越大，那么离均值欧氏距离远的点可能和之前分布中离得较近的点获得同样的马氏距离值。
所以本文中才引入了级联匹配的策略将遮挡时间按等级分层，遮挡时间越小的匹配等级更高，即更容易被匹配。
首先是得到追踪框集合T和检测框集合D，设置最大的Amax为轨迹最大允许丢失匹配的帧数。通过计算上面的评价指标（两种度量的加权和）得到成本矩阵，再通过级联条件，设定阈值分别对外观和位置因素进行计算，满足条件则返回1，否则返回0。然后初始化匹配矩阵为空，初始化未匹配矩阵等于D。通过匈牙利算法，对于每个属于追踪框集合的元素T，在检测框里面查找成本最低且满足阈值过滤条件的检测框作为匹配结果，同时更新匹配矩阵和非匹配矩阵。
在匹配的最后阶段还对unconfirmed和age=1的未匹配轨迹进行基于IOU的匹配。这可以缓解因为表观突变或者部分遮挡导致的较大变化。当然有好处就有坏处，这样做也有可能导致一些新产生的轨迹被连接到了一些旧的轨迹上。但这种情况较少。
深度表观描述子
预训练的网络时一个在大规模ReID数据集上训练得到的，这个ReID数据集包含1261个人的1100000幅图像，使得学到的特征很适合行人跟踪。
然后使用该预训练网络作为基础网络，构建wide ResNet，用来提取bounding box的表观特征。

匈牙利算法

（待补充）

卡尔曼滤波器

（待补充）

姿态估计

姿态估计综述

OpenPose

注意机制

self-attention

普通卷积将特征图的每个位置作为中心点，对该位置及其周围的位置进行加权求和，得到新的特征图上该位置对应的滤波结果，这一操作可以有效提取图片的局部信息。随着网络加深，卷积层不断堆叠，每个位置的感受域也越来越大，网络提取到的特征也逐渐由一些low-level的特征，如颜色、纹理，转变到一些high-level的结构信息。但是，简单通过加深网络来获取全局感受域，所带来的计算开销是很大的，并且更深的网络会带来更大的优化难度。
Self-attention操作可以有效地捕获不同位置之间的long-range dependency，每个位置的特征都由所有位置的加权求和得到，这里的权重就是attention weight，使得每个位置都可以获取全局的感受域。与传统的注意力机制不同，self-attention计算的是同一张图片中不同位置之间的注意力分配，从而提取该图片的特征。Self-attention机制在视觉任务解决了卷积神经网络的局部感受野问题，使得每个位置都可以获得全局的感受野。不过，由于在视觉任务中，像素数目极多，利用所有位置来计算每个位置的attention会导致巨大的计算和显存开销；另一方面，由于self-attention简单将图像当成一个序列进行处理，没有考虑不同位置之间的相对位置关系，使得所得到的attention丧失了图像的结构信息。
在NLP任务中，对于Attention机制的整个计算过程，可以总结为以下三个过程：
首先根据 Query 与 Key 计算两者之间的相似性或相关性， 即 socre 的计算。通过一个 softmax 来对值进行归一化处理获得注意力权重值， 即$a{i,j}$的计算。最后通过注意力权重值对value进行加权求和， 即$c{i,j}$ 的计算。

$$\alpha_{i,j} = \frac{e^{score(Query,Key(j))}}{\sum_{k=1}^te^{score(Query,Key(k))}}$$ $$c_i=\sum_{j=1}^n\alpha_{i,j}h_j$$

self attention本质上是为序列中每个元素都分配一个权重系数，这也可以理解为软寻址。如果序列中每一个元素都以(K,V)形式存储，那么attention则通过计算Q和K的相似度来完成寻址。Q和K计算出来的相似度反映了取出来的V值的重要程度，即权重，然后加权求和就得到了attention值。
引入Self Attention后会更容易捕获句子中长距离的相互依赖的特征，因为如果是RNN或者LSTM，需要依次序序列计算，对于远距离的相互依赖的特征，要经过若干时间步步骤的信息累积才能将两者联系起来，而距离越远，有效捕获的可能性越小。
但是Self Attention在计算过程中会直接将句子中任意两个单词的联系通过一个计算步骤直接联系起来，所以远距离依赖特征之间的距离被极大缩短，有利于有效地利用这些特征。除此外，Self Attention对于增加计算的并行性也有直接帮助作用。这是为何Self Attention逐渐被广泛使用的主要原因。

scale attention

视觉任务中另一类注意力机制为scale attention。与self-attention不同，scale attention基于每个位置本身的响应。就分类任务而言，每个位置的响应越大，则其对于最终的分类结果影响越大，那么这个位置本身的重要性就越强。根据响应大小有选择地对特征图进行强化或抑制，就可以在空间（或其他维度）上达到分配attention的目的。例如SENet，就相当于channel-wise的attention。这一类注意力机制仅仅基于图像中每个位置本身，对显著区域进行增强，非显著区域进行抑制，比self-attention机制更接近与人类视觉系统的注意力机制。

Bottom-up and top-down形式的scale attention

在分类网络中，网络深层比浅层更关注于被分类的物体，也就是图片的主体内容，这是因为，深层网络具有更大的视野域，可以看到更广的范围；而浅层网络只能看到每个位置及其邻域。因此，如果将网络较深层的信息作为一种mask，作用在较浅层的特征上，就能更好的增强浅层特征中对于最终分类结果有帮助的特征，抑制不相关的特征。如图5所示，将attention作为mask作用在原来特征上，得到的输出就会更加集中在对分类有帮助的区域上。

文章提出一种bottom-up top-down的前向传播方法来得到图片的attention map，并且将其作用在原来的特征上，使得输出的特征有更强的区分度。图6展示了这种attention的计算方式。由于更大的视野域可以看到更多的内容，从而获得更多的attention信息，因此，作者设计了一条支路，通过快速下采样和上采样来提前获得更大的视野域，将输出的特征进行归一化后作用在原有的特征上，将作用后的特征以残差的形式加到原来的特征上，就完成了一次对原有特征的注意力增强。文章还提出了一个堆叠的网络结构，即residual attention network，中间多次采用这种attention模块进行快速下采样和上采样。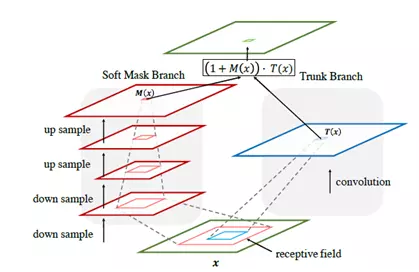

Squeeze and excite形式的注意力

与residual attention不同，squeeze-and-excite通过global pooling来获得全局的视野域，并将其作为一种指导的信息，也就是attention信息，作用到原来的特征上。
SENet提出了channel-wise的scale attention。特征图的每个通道对应一种滤波器的滤波结果，即图片的某种特定模式的特征。对于最终的分类结果，这些模式的重要性是不同的，有些模式更重要，因此其全局的响应更大；有些模式不相关，其全局的响应较小。通过对不同通道的特征根据其全局响应值，进行响应的增强或抑制，就可以起到在channel上进行注意力分配的作用。其网络结构如图7所示，首先对输入特征进行global pooling，即为squeeze阶段，对得到的特征进行线性变换，即为excite阶段，最后将变换后的向量通过广播，乘到原来的特征图上，就完成了对不同通道的增强或抑制。

作为SENet的一个延续，convolutional block attention module （CBAM）将SENet中提出的channel attention扩展到了spatial attention上，通过一个串行的支路，将channel attention和spatial attention连接起来，对原特征进行增强。其网络结构如图9所示，首先进行channel attention，对通道进行增强和抑制，这一过程与SENet的操作完全相同，然后在每个位置上进行通道的squeeze和excite操作，得到与原特征图一样分辨率的1通道spatial attention，再作用到原特征图上，即为spatial attention操作。最终的输出即为spatial attention module的输出。相比SENet，CBAM带来的性能提升有限，在该模块中其主要作用的还是channel attention模块。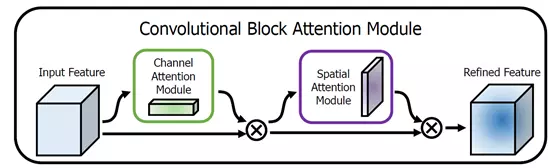

多分类

序列神经网络

LSTM

RNN相对传统的ANN网络结构实现了信息的保留，具有一定的记忆功能。可以将过去的信息应用到当前的任务中。
下图展示了RNN的闭环结构和开环结构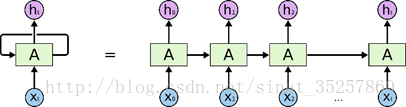

完成当前任务如果仅仅需要短期的信息而不需要长期的信息可以使用RNN。但是如果任务需要更多的上下文信息，仅仅依靠少量的过去信息无法完成准确的预测。也就是过去信息和当前任务存在较大的跳动，甚至需要未来的信息才能完成预测。这时经典的RNN就无法满足需要,而需要特殊的时间序列模型LSTM。LSTMs 就是用来解决长期依赖问题，这类模型可以记住长期信息。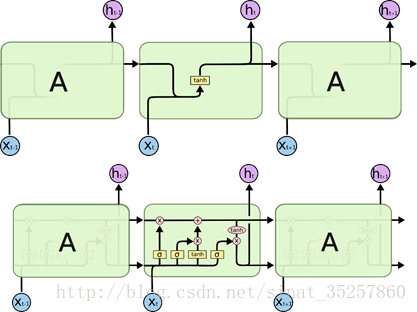

典的RNN模型中的激活函数可能就是一个简单的tanh函数，但是LSTMs引入了四个门结构，具有增加或者移除信息状态的功能。门限可以有选择的让信息通过，它是由sigmoid神经网络层和pointwise乘法操作构成的。sigmoid层输入数值0-1 代表可以通过的比例，输入为0时代表不允许通过，输出为1时代表允许全部通过。
1）forget gate 遗忘门

遗忘门输入是$h{t-1}$，输出是$f_t$，$f_t$作用于$C{t-1}$。当$ft$为1时，代表保留该值，当$f_t$为0时，代表完全舍去该值。
2）input gate 输入门

存储什么样的新信息包括两步，第一步输入门决定哪些值可以更新，第二步tanh层创造候选向量。$i_t$是sigmoid函数输出结果表示是否产生输入，其取值范围是0-1。$\tilde{C_t}$是新产生的候选向量。忘记门$f_t$乘$C{t-1}$：忘掉决定忘掉的早期信息，其结果加上$i_t * \tilde{C_t}$，候选向量通过$i_t$缩放后表示多大程度上更新状态值。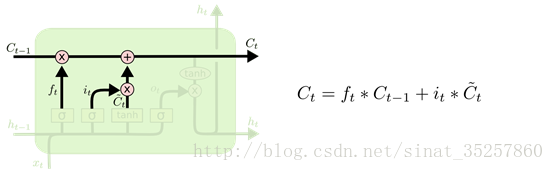

通过忘记门和输入门的组合可以表达出这样的信息：多大程度上忘记旧的信息以及多大程度上更新新的信息。
3）Output gate 输出门

首先sigmoid函数决定输出的缩放比例$o_t$，然后cell 状态通过tanh函数，其结果与$o_t$相乘。

RNN、LSTM、GRU区别

RNN引入了循环的概念，但是在实际过程中却出现了初始信息随时间消失的问题，即长期依赖（Long-Term Dependencies）问题，所以引入了LSTM。
LSTM：因为LSTM有进有出且当前的cell informaton是通过input gate控制之后叠加的，RNN是叠乘，因此LSTM可以防止梯度消失或者爆炸。
GRU是LSTM的变体，将忘记门和输入们合成了一个单一的更新门。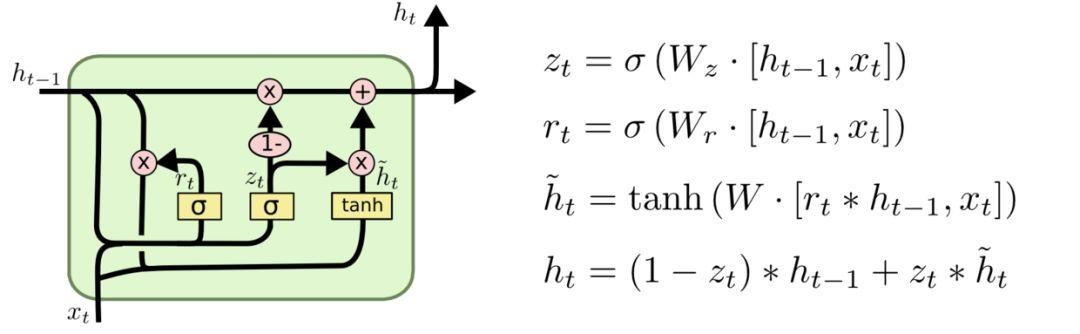

LSTM防止梯度消失和爆炸

LSTM用加和的方式取代了乘积，使得很难出现梯度弥散。但是相应的更大的几率会出现梯度爆炸，但是可以通过给梯度加门限解决这一问题。

TCN

时序问题的建模大家一般习惯性的采用循环神经网络（RNN）来建模，这是因为RNN天生的循环自回归的结构是对时间序列的很好的表示。传统的卷积神经网络一般认为不太适合时序问题的建模，这主要由于其卷积核大小的限制，不能很好的抓取长时的依赖信息。一种特殊的卷积神经网络——时序卷积网络（Temporal convolutional network， TCN）与多种RNN结构相对比，发现在多种任务上TCN都能达到甚至超过RNN模型。

因果卷积(Causal Convolution)

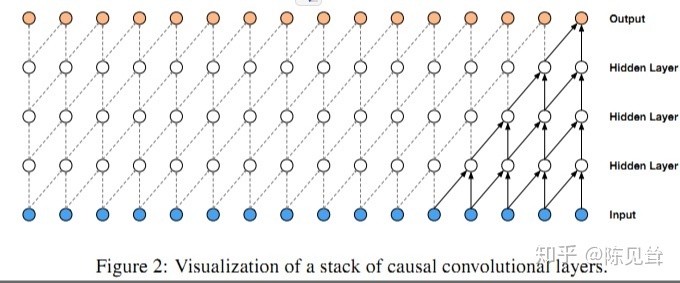
因果卷积可以用上图直观表示。 即对于上一层t时刻的值，只依赖于下一层t时刻及其之前的值。和传统的卷积神经网络的不同之处在于，因果卷积不能看到未来的数据，它是单向的结构，不是双向的。也就是说只有有了前面的因才有后面的果，是一种严格的时间约束模型，因此被成为因果卷积。

膨胀卷积(Dilated Convolution)

单纯的因果卷积还是存在传统卷积神经网络的问题，即对时间的建模长度受限于卷积核大小的，如果要想抓去更长的依赖关系，就需要线性的堆叠很多的层。为了解决这个问题，研究人员提出了膨胀卷积。如下图所示。

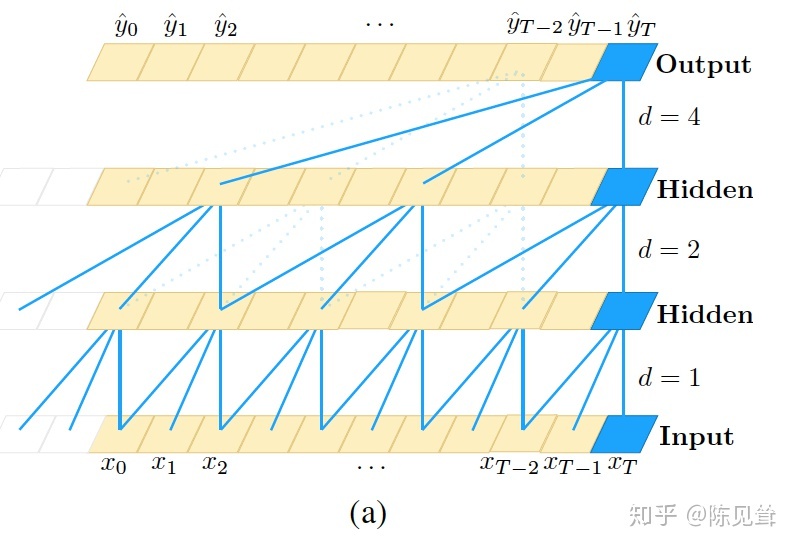
和传统卷积不同的是，膨胀卷积允许卷积时的输入存在间隔采样，采样率受图中的d控制。 最下面一层的d=1，表示输入时每个点都采样，中间层d=2，表示输入时每2个点采样一个作为输入。一般来讲，越高的层级使用的d的大小越大。所以，膨胀卷积使得有效窗口的大小随着层数呈指数型增长。这样卷积网络用比较少的层，就可以获得很大的感受野。

$$F(s)=\sum_{i=0}^{k-1}f(i)\cdot x_{s-d\cdot i}$$

空洞卷积

残差连接(Residual Connections)

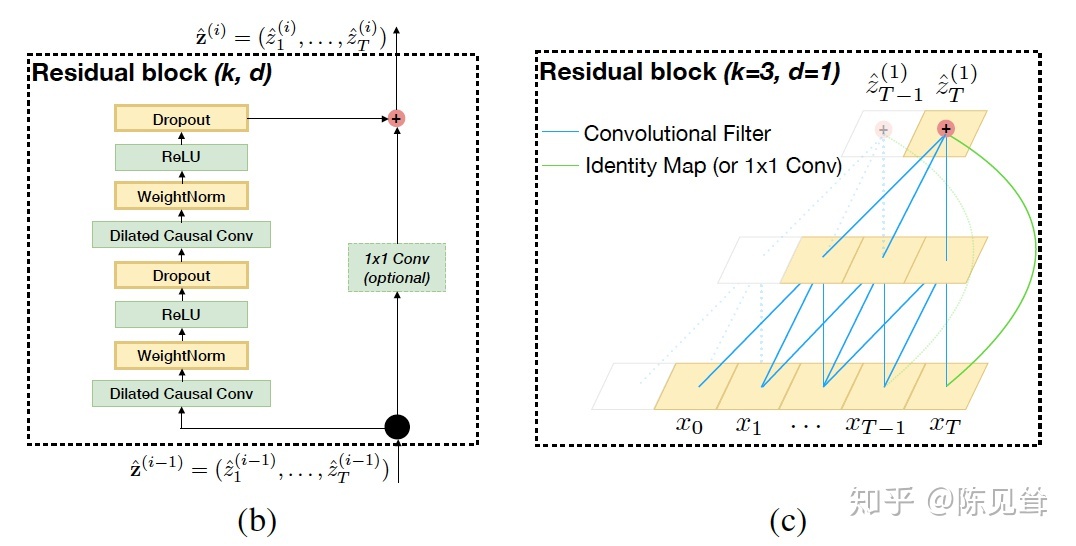
残差链接被证明是训练深层网络的有效方法，它使得网络可以以跨层的方式传递信息。本文构建了一个残差块来代替一层的卷积。如上图所示，一个残差块包含两层的卷积和非线性映射，在每层中还加入了WeightNorm和Dropout来正则化网络。

TCN优点和缺点

优点
（1）并行性。当给定一个句子时，TCN可以将句子并行的处理，而不需要像RNN那样顺序的处理。
（2）灵活的感受野。TCN的感受野的大小受层数、卷积核大小、扩张系数等决定。可以根据不同的任务不同的特性灵活定制。
（3）稳定的梯度。RNN经常存在梯度消失和梯度爆炸的问题，这主要是由不同时间段上共用参数导致的，和传统卷积神经网络一样，TCN不太存在梯度消失和爆炸问题。
（4）内存更低。RNN在使用时需要将每步的信息都保存下来，这会占据大量的内存，TCN在一层里面卷积核是共享的，内存使用更低。
缺点
（1）TCN 在迁移学习方面可能没有那么强的适应能力。这是因为在不同的领域，模型预测所需要的历史信息量可能是不同的。因此，在将一个模型从一个对记忆信息需求量少的问题迁移到一个需要更长记忆的问题上时，TCN 可能会表现得很差，因为其感受野不够大。
（2）论文中描述的TCN还是一种单向的结构，在语音识别和语音合成等任务上，纯单向的结构还是相当有用的。但是在文本中大多使用双向的结构，当然将TCN也很容易扩展成双向的结构，不使用因果卷积，使用传统的卷积结构即可。
（3）TCN毕竟是卷积神经网络的变种，虽然使用扩展卷积可以扩大感受野，但是仍然受到限制，相比于Transformer那种可以任意长度的相关信息都可以抓取到的特性还是差了点。TCN在文本中的应用还有待检验。

图网络

图卷积网络
卷积是通过计算中心像素点以及相邻像素点的加权和来构成feature map实现空间特征提取。图卷积主要分为空域图卷积和谱域图卷积。
空域图卷积，其思想是将每个节点与其相邻节点的特征进行加权，使用领域来确定每个节点的加权平均范围（卷积范围），使用label策略来为参与卷积的节点分配权重，其层间传播矩阵为：

$$X^{l+1}=\delta(W^lX^lA)$$

其中A是邻接矩阵，包含邻居节点信息，A中节点相连为1否则为0。通过矩阵乘法可以使得每个节点和其邻居节点特征进行聚合。W是权重矩阵，主要是对边进行加权。这样的传播方法是没有对邻接矩阵进行归一化，这使得A在传播过程中不断扩张（每次乘A会导致特征值越来越大）。此外，由于A对角线元素为0，每个节点自身在进行卷积时不能将自己的特征计算在内。因此，在空域图卷积中引入了谱域图卷积的思想来解决这两个问题。谱域图卷积主要借助图的拉普拉斯矩阵和傅里叶变换来进行的，最后得到的层间传播公式为：

$$X^{l+1}=\delta(\land^{(-\frac{1}{2})}(A+I)\land^{(-\frac{1}{2})}X^lW^l)$$

其中矩阵$\land$用于对扩展邻接矩阵(A+I)进行归一化。
首先和单纯的空域图卷积相比，对邻接矩阵做了自环操作(A+I)，通过加单位矩阵的方法，使得中心节点自身的特征能参与卷积。然后通过对邻接矩阵实现归一化，解决了A随层数不断增长的问题。其他的部分就和公式(1)完全一致了。因此我们可以说公式(2)是利用谱域图卷积的思想来弥补了空域图卷积的缺点，本质上是两种卷积思想的结合。

图像处理方法

Canny边缘检测

Canny边缘检测是通过灰度值的变化（梯度）来判断边缘信息的。主要包含以下四个步骤：
1）高斯滤波
滤波的主要目的是降噪，一般的图像处理算法都需要先进行降噪。而高斯滤波主要使图像变得平滑（模糊），同时也有可能增大了边缘的宽度。
对于一个位置（m,n）的像素点，其灰度值（这里只考虑二值图）为f(m,n)。那么经过高斯滤波后的灰度值将变为：

$$g_{\sigma}(m,n)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{m^2+n^2}{2\sigma^2}}f(m,n)$$

简单说就是用一个高斯矩阵乘以每一个像素点及其邻域，取其带权重的平均值作为最后的灰度值。
2）计算梯度值和梯度方向
边缘就是灰度值变化较大的的像素点的集合。在图像中，用梯度来表示灰度值的变化程度和方向。
它可以通过点乘一个sobel或其它算子得到不同方向的梯度值 $g_x(m,n)$ , $g_y(m,n)$ 。
综合梯度通过以下公式计算梯度值和梯度方向：

$$G(m,n)=\sqrt{g_x(m,n)^2+g_y(m,n)^2}$$ $$\theta=arctan \frac{g_y(m,n)}{g_x(m,n)}$$

3）过滤非最大值
在高斯滤波过程中，边缘有可能被放大了。这个步骤使用一个规则来过滤不是边缘的点，使边缘的宽度尽可能为1个像素点：如果一个像素点属于边缘，那么这个像素点在梯度方向上的梯度值是最大的。否则不是边缘，将灰度值设为0。

$$M_T(m,n)=\begin{cases} M(m,n) \ if\ M(m,n)>T \\ 0 \ otherwise \end{cases}$$

4）使用上下阈值来检测边缘
一般情况下，使用一个阀值来检测边缘，但是这样做未免太武断了。如果能够使用启发式的方法确定一个上阀值和下阀值，位于下阀值之上的都可以作为边缘，这样就可能提高准确度。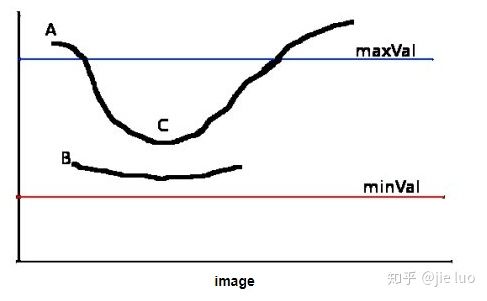

它设置两个阀值（threshold），分别为maxVal和minVal。其中大于maxVal的都被检测为边缘，而低于minval的都被检测为非边缘。对于中间的像素点，如果与确定为边缘的像素点邻接，则判定为边缘；否则为非边缘。